Tiles Puzzle and Algebra
July 23rd , 2024 by Rohan Rao
Flip Puzzle
I was playing some puzzles from Simon Tatham’s Portable Puzzle Collection and I came across a puzzle called ‘Flip’.
The puzzle starts with a grid of black and white squares. You have the ability to click squares, and when you click a square the square, and the squares sharing an edge with it flip color (the ‘cross’ flips color).
The object of the game is to flip all the squares to white.
Here’s an animation of solving a 5 x 5 version of the puzzle.
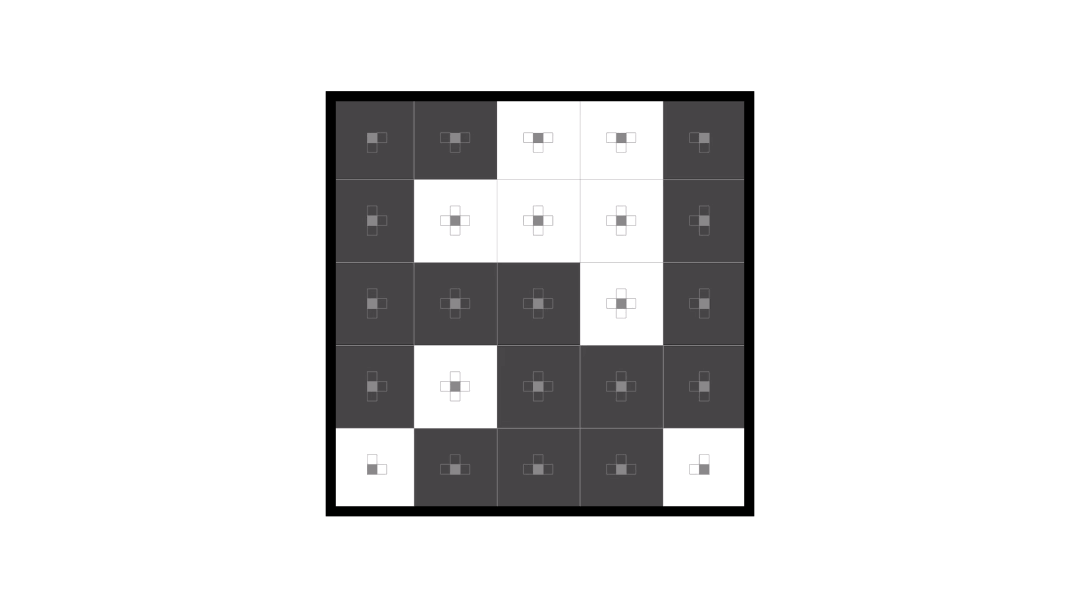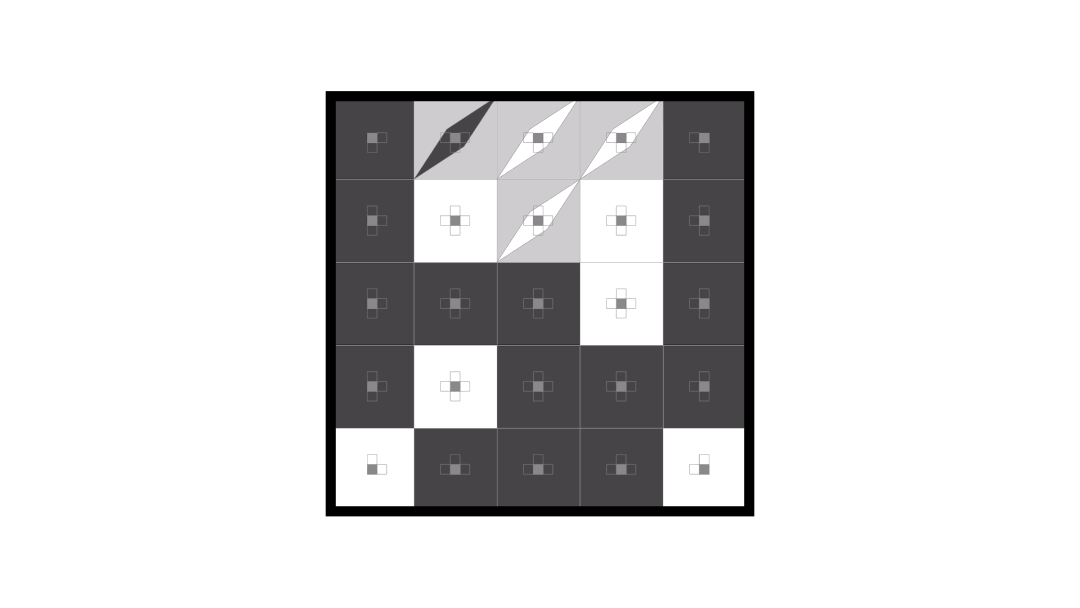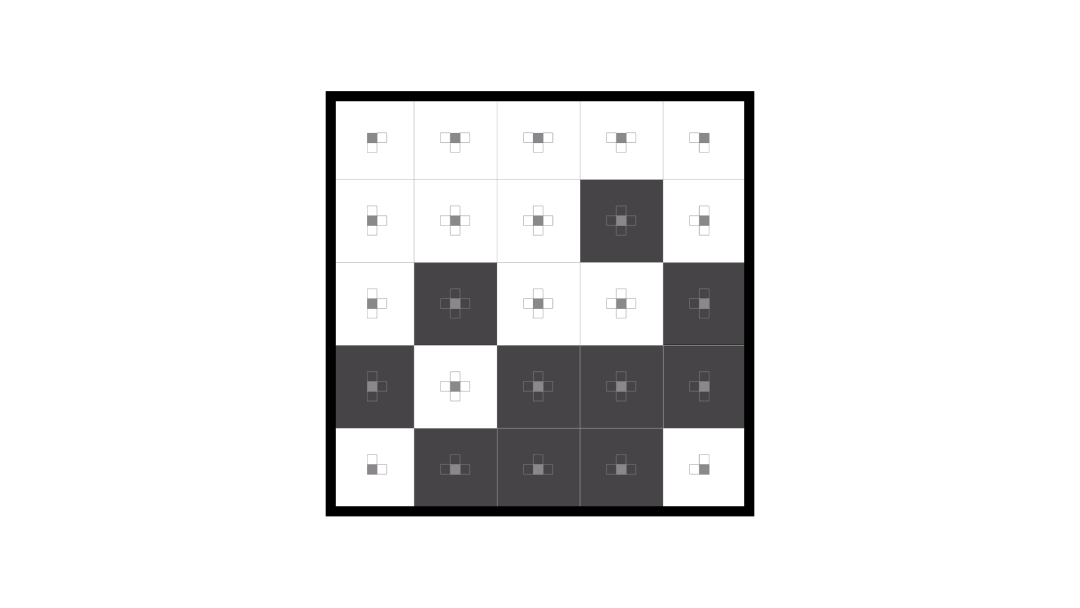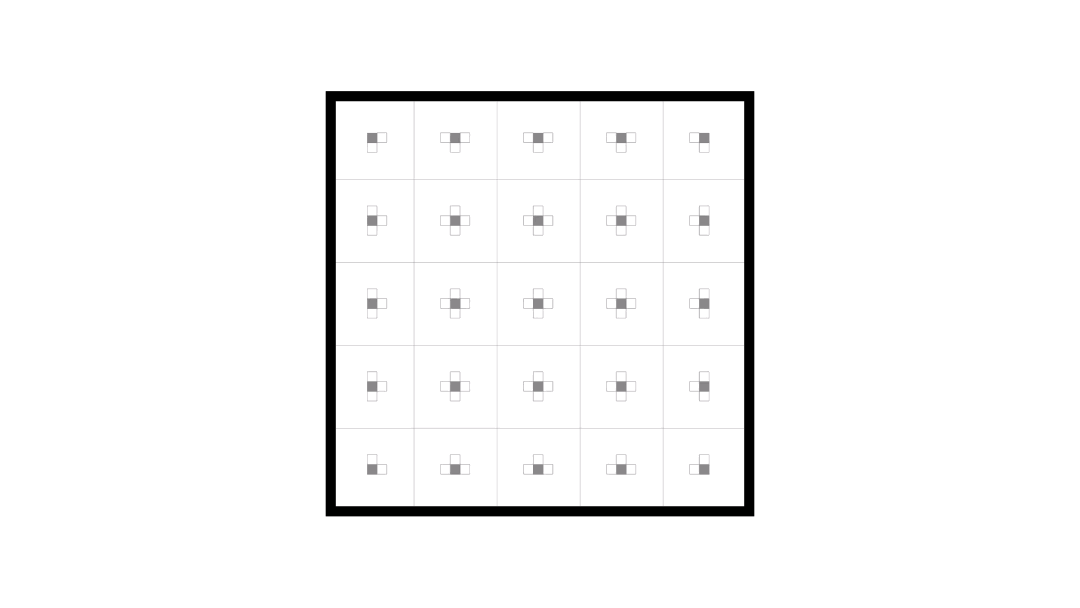
I wanted to think of a general solution to reasoning about this sort of puzzle and here’s what I came up with.
To start with here are a few observations about this game:
- the order in which you flip segments doesn’t matter (So a solution can be uniquely represented by which squares need to be clicked)
- only the parity of the number of times a square is flipped (by clicking any square) matters. If the square starts off black you want to flip it an odd number of times otherwise you want to flip it an even number of times. Relatedly it only matters whether a square is clicked an odd or even number of times (so 0 times or 1 time)
Going further we can think of the puzzle

as being something like
“I want to flip square \((0,0)\) an even number of times, .. I want to flip square \((0,3)\) an odd number of times … by clicking square \((0,0)\) \(x_1\) times, and square \((0,1)\) \(x_2\) times…”
where \(x_i\) is \(0\) or \(1\).
This is just a system of linear equations in mod 2 space \(GF(2)\)!
The Equations
More formally here’s how to set up the system.
lets start with an \(n\) x \(n\) board \(B_n\) with squares labeled \(b_i\)
\[B = \begin{bmatrix} b_{1} & \dots & b_n \\ \vdots & \ddots & \\ b_{n^2 - n + 1} & & b_{n^2} \end{bmatrix}\]Now lets set up another matrix \(A\)
\[A = \begin{bmatrix} a_{1,1} & \dots & a_{1,n^2} \\ \vdots & \ddots & \\ a_{n^2,1} & & a_{n^2,n^2} \end{bmatrix}\]where \(a_{i,j} = 1\) if clicking square \(j\) would flip square \(i\).
Then we want to solve the system for \(f_i\) (all in mod 2 or \(GF(2)\))
\[\begin{bmatrix} a_{1,1} & \dots & a_{1,n^2} \\ \vdots & \ddots & \\ a_{n^2,1} & & a_{n^2,n^2} \end{bmatrix} \begin{bmatrix} f_1 \\ \vdots \\ f_{n^2} \end{bmatrix} = \begin{bmatrix} b_1 \\ \vdots \\ b_{n^2} \end{bmatrix}\]and \(f_i = 1\) means we click that square (otherwise don’t click).
To make this more tangible, for a 3 x 3 grid,
\[A = \displaystyle \left[\begin{matrix}1 & 1 & 0 & 1 & 0 & 0 & 0 & 0 & 0\\1 & 1 & 1 & 0 & 1 & 0 & 0 & 0 & 0\\0 & 1 & 1 & 0 & 0 & 1 & 0 & 0 & 0\\1 & 0 & 0 & 1 & 1 & 0 & 1 & 0 & 0\\0 & 1 & 0 & 1 & 1 & 1 & 0 & 1 & 0\\0 & 0 & 1 & 0 & 1 & 1 & 0 & 0 & 1\\0 & 0 & 0 & 1 & 0 & 0 & 1 & 1 & 0\\0 & 0 & 0 & 0 & 1 & 0 & 1 & 1 & 1\\0 & 0 & 0 & 0 & 0 & 1 & 0 & 1 & 1\end{matrix}\right]\]For example if we reshape the 5th column of this (corresponding to clicking the middle squuare of the 3x3 grid)
\[a_{:,5} = \displaystyle \left[\begin{matrix}0\\1\\0\\1\\1\\1\\0\\1\\0\end{matrix}\right] \rightarrow \displaystyle \left[\begin{matrix}0 & 1 & 0\\1 & 1 & 1\\0 & 1 & 0\end{matrix}\right]\]which makes sense because clicking the middle square leads to flipping the middle cross.
Just for fun here’s the A matrix for a 4x4 grid
\[A_4 = \displaystyle \left[\begin{array}{cccccccccccccccc}1 & 1 & 0 & 0 & 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0\\1 & 1 & 1 & 0 & 0 & 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0\\0 & 1 & 1 & 1 & 0 & 0 & 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0\\0 & 0 & 1 & 1 & 0 & 0 & 0 & 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0\\1 & 0 & 0 & 0 & 1 & 1 & 0 & 0 & 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0\\0 & 1 & 0 & 0 & 1 & 1 & 1 & 0 & 0 & 1 & 0 & 0 & 0 & 0 & 0 & 0\\0 & 0 & 1 & 0 & 0 & 1 & 1 & 1 & 0 & 0 & 1 & 0 & 0 & 0 & 0 & 0\\0 & 0 & 0 & 1 & 0 & 0 & 1 & 1 & 0 & 0 & 0 & 1 & 0 & 0 & 0 & 0\\0 & 0 & 0 & 0 & 1 & 0 & 0 & 0 & 1 & 1 & 0 & 0 & 1 & 0 & 0 & 0\\0 & 0 & 0 & 0 & 0 & 1 & 0 & 0 & 1 & 1 & 1 & 0 & 0 & 1 & 0 & 0\\0 & 0 & 0 & 0 & 0 & 0 & 1 & 0 & 0 & 1 & 1 & 1 & 0 & 0 & 1 & 0\\0 & 0 & 0 & 0 & 0 & 0 & 0 & 1 & 0 & 0 & 1 & 1 & 0 & 0 & 0 & 1\\0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 1 & 0 & 0 & 0 & 1 & 1 & 0 & 0\\0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 1 & 0 & 0 & 1 & 1 & 1 & 0\\0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 1 & 0 & 0 & 1 & 1 & 1\\0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 1 & 0 & 0 & 1 & 1\end{array}\right]\]An ill advised 5x5 matrix
\[A_5 = \displaystyle \left[\begin{array}{ccccccccccccccccccccccccc}1 & 1 & 0 & 0 & 0 & 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0\\1 & 1 & 1 & 0 & 0 & 0 & 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0\\0 & 1 & 1 & 1 & 0 & 0 & 0 & 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0\\0 & 0 & 1 & 1 & 1 & 0 & 0 & 0 & 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0\\0 & 0 & 0 & 1 & 1 & 0 & 0 & 0 & 0 & 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0\\1 & 0 & 0 & 0 & 0 & 1 & 1 & 0 & 0 & 0 & 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0\\0 & 1 & 0 & 0 & 0 & 1 & 1 & 1 & 0 & 0 & 0 & 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0\\0 & 0 & 1 & 0 & 0 & 0 & 1 & 1 & 1 & 0 & 0 & 0 & 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0\\0 & 0 & 0 & 1 & 0 & 0 & 0 & 1 & 1 & 1 & 0 & 0 & 0 & 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0\\0 & 0 & 0 & 0 & 1 & 0 & 0 & 0 & 1 & 1 & 0 & 0 & 0 & 0 & 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0\\0 & 0 & 0 & 0 & 0 & 1 & 0 & 0 & 0 & 0 & 1 & 1 & 0 & 0 & 0 & 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0\\0 & 0 & 0 & 0 & 0 & 0 & 1 & 0 & 0 & 0 & 1 & 1 & 1 & 0 & 0 & 0 & 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0\\0 & 0 & 0 & 0 & 0 & 0 & 0 & 1 & 0 & 0 & 0 & 1 & 1 & 1 & 0 & 0 & 0 & 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0\\0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 1 & 0 & 0 & 0 & 1 & 1 & 1 & 0 & 0 & 0 & 1 & 0 & 0 & 0 & 0 & 0 & 0\\0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 1 & 0 & 0 & 0 & 1 & 1 & 0 & 0 & 0 & 0 & 1 & 0 & 0 & 0 & 0 & 0\\0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 1 & 0 & 0 & 0 & 0 & 1 & 1 & 0 & 0 & 0 & 1 & 0 & 0 & 0 & 0\\0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 1 & 0 & 0 & 0 & 1 & 1 & 1 & 0 & 0 & 0 & 1 & 0 & 0 & 0\\0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 1 & 0 & 0 & 0 & 1 & 1 & 1 & 0 & 0 & 0 & 1 & 0 & 0\\0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 1 & 0 & 0 & 0 & 1 & 1 & 1 & 0 & 0 & 0 & 1 & 0\\0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 1 & 0 & 0 & 0 & 1 & 1 & 0 & 0 & 0 & 0 & 1\\0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 1 & 0 & 0 & 0 & 0 & 1 & 1 & 0 & 0 & 0\\0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 1 & 0 & 0 & 0 & 1 & 1 & 1 & 0 & 0\\0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 1 & 0 & 0 & 0 & 1 & 1 & 1 & 0\\0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 1 & 0 & 0 & 0 & 1 & 1 & 1\\0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 1 & 0 & 0 & 0 & 1 & 1\end{array}\right]\]This approach can be used for any similar puzzle (not just crosses) and can be used to find what to click to transform any board state into another (if possible).
Solving the Equations
solving linear equations in \(GF(2)\) is pretty similar to solving them over \(\mathbb{R}\)
With standard linear equations you form an augmented matrix and row reduce it. The reduced matrix will tell us the free variables we have and give us solutions to the system in terms of the free variables. While reducing the matrix in \(GF(2)\) you are allowed to switch rows, and add one row to another. (in \(\mathbb{R}\) you can scale by a constant but in \(GF(2)\) there’s only 0 and 1 so this step isn’t needed). As an implementation note, adding a row to another is equivalent to element wise XOR.
As a note: The internet suggests using sympy with a “zerofunction” lambda that maps numbers mod 2 to 0 (https://stackoverflow.com/questions/31190182/sympy-solving-matrices-in-a-finite-field) which I tried at first but the result didn’t seem correct to me. Without much investigation it kind of looked like this approach does standard row reduction in \(\mathbb{R}\) and then takes \(\mod(2)\) of the results at the intermediate steps. I think this might not be right because it would allow doing stuff like multiplying by \(\frac{1}{2}\) and then taking \(\mod(2)\) which is illegal.
Our matrix is considered reduced when the leading number in each row is 1 and is the only nonzero number in its column or the row is all zeros.
We can hand implement doing this with elementary row operations. Start with the first column and find a row with a 1 in the first column. Swap this to the top position and add it to all the other rows with a 1 in the first column. Next find a row with a 1 in the second column and a zero in the first column. Then swap it into position and add it to the other rows with a 1 in the second column, etc. If theres no row for a specific column, just skip it and move on.
Lets solve a 4x4 matrix for example.

Starting with the augmented matrix \(A \mid b\) where A is our coefficient matrix and b is our board
and then reducing it with row operations
\[[A'|b'] = \displaystyle \left[\begin{matrix}1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 1 & 1 & 1\\0 & 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 1 & 1 & 0 & 1\\0 & 0 & 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 1 & 0 & 1 & 1\\0 & 0 & 0 & 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 1 & 1 & 1 & 0\\0 & 0 & 0 & 0 & 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 1 & 0 & 1 & 0\\0 & 0 & 0 & 0 & 0 & 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 1\\0 & 0 & 0 & 0 & 0 & 0 & 1 & 0 & 0 & 0 & 0 & 0 & 1 & 0 & 0 & 0\\0 & 0 & 0 & 0 & 0 & 0 & 0 & 1 & 0 & 0 & 0 & 0 & 0 & 1 & 0 & 1\\0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 1 & 0 & 0 & 0 & 1 & 1 & 0 & 0\\0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 1 & 0 & 0 & 1 & 1 & 1 & 0\\0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 1 & 0 & 0 & 1 & 1 & 1\\0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 1 & 0 & 0 & 1 & 1\\0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0\\0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0\\0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0\\0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0\end{matrix} \left| \, \begin{matrix}0\\1\\1\\0\\1\\0\\0\\1\\0\\1\\1\\1\\0\\0\\0\\0\end{matrix} \right. \right]\]where our reduced system of equation representing the problem is \(A'f = b'\)
One important note is that \(A'\) doesn’t depend on \(b\), it just depends on \(A\). Additionally non-\(b'\) columns that don’t have a single \(1\) in them (and the rest \(0\)s) represent free variables in our solution. We can pick any values for the variables corresponding to those columns. Once we pick values for those variables we can easily solve for the non-free variables.
Lets pick 0’s for the free variables (just arbitrarily - we can get other solutions by picking 1 for the free variables / free squares).
Now things simplify to \(\displaystyle \left[\begin{array}{cccccccccccc}1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0\\0 & 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0\\0 & 0 & 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0\\0 & 0 & 0 & 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0\\0 & 0 & 0 & 0 & 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0\\0 & 0 & 0 & 0 & 0 & 1 & 0 & 0 & 0 & 0 & 0 & 0\\0 & 0 & 0 & 0 & 0 & 0 & 1 & 0 & 0 & 0 & 0 & 0\\0 & 0 & 0 & 0 & 0 & 0 & 0 & 1 & 0 & 0 & 0 & 0\\0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 1 & 0 & 0 & 0\\0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 1 & 0 & 0\\0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 1 & 0\\0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 1\\0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0\\0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0\\0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0\\0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0\end{array}\right] \begin{bmatrix} f_1 \\ \vdots \\ f_{12} \end{bmatrix} = \left[\begin{matrix}0\\1\\1\\0\\1\\0\\0\\1\\0\\1\\1\\1\\0\\0\\0\\0\end{matrix}\right]\)
Which results in \(\begin{bmatrix} f_1 \\ \vdots \\ f_{16} \end{bmatrix} = \left[\begin{matrix}0\\1\\1\\0\\1\\0\\0\\1\\0\\1\\1\\1\\0\\0\\0\\0\end{matrix}\right]\)
which means we should click the followings squares (reshaping the solution)!
\[\displaystyle \left[\begin{matrix}0 & 1 & 1 & 0\\1 & 0 & 0 & 1\\0 & 1 & 1 & 1\\0 & 0 & 0 & 0\end{matrix}\right]\]Lets try it out!

Some Resulting Consequences + Observations
Result: Each 4x4 puzzle has 16 solutions or no solutions
because there are 4 free variables that can be 1 or 0 (the last 4 columns of \(A'_4\))
Result: There is always a solution to a 4x4 puzzle without using the bottom row (similarly a solution not using the top row or left row or right row)
because we can choose 0s for the free variables (which are squares 13-16). And we can rotate the puzzle and solve and rotate back to get the solutions not using the left, top, or right row respectively
Result: Not Every 4x4 puzzle has a solution
For example
\[B = \displaystyle \left[\begin{matrix}0 & 0 & 1 & 0\\1 & 1 & 1 & 0\\0 & 0 & 1 & 1\\0 & 1 & 1 & 1\end{matrix}\right]\]after we look at the reduced system
\[[A'|b'] = \displaystyle \left[\begin{matrix}1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 1 & 1 & 1\\0 & 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 1 & 1 & 0 & 1\\0 & 0 & 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 1 & 0 & 1 & 1\\0 & 0 & 0 & 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 1 & 1 & 1 & 0\\0 & 0 & 0 & 0 & 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 1 & 0 & 1 & 0\\0 & 0 & 0 & 0 & 0 & 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 1\\0 & 0 & 0 & 0 & 0 & 0 & 1 & 0 & 0 & 0 & 0 & 0 & 1 & 0 & 0 & 0\\0 & 0 & 0 & 0 & 0 & 0 & 0 & 1 & 0 & 0 & 0 & 0 & 0 & 1 & 0 & 1\\0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 1 & 0 & 0 & 0 & 1 & 1 & 0 & 0\\0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 1 & 0 & 0 & 1 & 1 & 1 & 0\\0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 1 & 0 & 0 & 1 & 1 & 1\\0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 1 & 0 & 0 & 1 & 1\\0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0\\0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0\\0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0\\0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0\end{matrix} \left| \, \begin{matrix}0\\0\\0\\1\\0\\0\\0\\1\\1\\1\\0\\0\\1\\0\\1\\1\end{matrix} \right. \right]\]has no solutions (bottom rows are \(0= 1\))
Result: Each 3x3 puzzle is solvable with a unique solution
\(A_3\) is invertible with inverse \(A_3^{-1} = \displaystyle \left[\begin{matrix}1 & 0 & 1 & 0 & 0 & 1 & 1 & 1 & 0\\0 & 0 & 0 & 0 & 1 & 0 & 1 & 1 & 1\\1 & 0 & 1 & 1 & 0 & 0 & 0 & 1 & 1\\0 & 0 & 1 & 0 & 1 & 1 & 0 & 0 & 1\\0 & 1 & 0 & 1 & 1 & 1 & 0 & 1 & 0\\1 & 0 & 0 & 1 & 1 & 0 & 1 & 0 & 0\\1 & 1 & 0 & 0 & 0 & 1 & 1 & 0 & 1\\1 & 1 & 1 & 0 & 1 & 0 & 0 & 0 & 0\\0 & 1 & 1 & 1 & 0 & 0 & 1 & 0 & 1\end{matrix}\right]\)
so we can always solve the system by applying the inverse
Result: Each 5x5 puzzle has at most 4 solutions
Similar argument to the 4x4 version.
\[A'_5 = \displaystyle \left[\begin{array}{ccccccccccccccccccccccccc}1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 1\\0 & 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 1 & 0\\0 & 0 & 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 1 & 1\\0 & 0 & 0 & 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 1 & 0\\0 & 0 & 0 & 0 & 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 1\\0 & 0 & 0 & 0 & 0 & 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 1 & 1\\0 & 0 & 0 & 0 & 0 & 0 & 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0\\0 & 0 & 0 & 0 & 0 & 0 & 0 & 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 1 & 1\\0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0\\0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 1 & 1\\0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 1 & 0\\0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 1 & 0\\0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0\\0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 1 & 0\\0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 1 & 0\\0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 1 & 1\\0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0\\0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 1 & 0 & 0 & 0 & 0 & 0 & 1 & 1\\0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 1 & 0 & 0 & 0 & 0 & 0 & 0\\0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 1 & 0 & 0 & 0 & 1 & 1\\0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 1 & 0 & 0 & 0 & 1\\0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 1 & 0 & 1 & 0\\0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 1 & 1 & 1\\0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0\\0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0\end{array}\right]\]where we have 2 free variables (last two columns). Also can conclude that all 5x5 puzzles aren’t solvable
Easy Way to get ‘a’ Solution
Since given a matrix \(A\) the steps we take to row reduce the matrix remain the same no matter what \(b\) is, if we just want the solution to the puzzle setting the free variables in our formulation to \(0\) (though can use a similar method for any choice of what we set the free variables to), we can construct a matrix \(C\) such that if we reduce \([A \mid b] \rightarrow [A' \mid b']\), then \(b' = Cb\).
Then if we remember \(C\) and know the puzzle is solvable, we can solve the puzzle by multiplying \(C\) by the initial board \(b\).
We can compute this by reducing \([A \mid I]->[A' \mid C]\) where \(I\) is the identity matrix.
for 3x3 puzzles \(C\) is the inverse mentioned above.
For 4x4 puzzles:
\[C_4 = \displaystyle \left[\begin{array}{cccccccccccccccc}1 & 1 & 0 & 0 & 1 & 0 & 1 & 0 & 0 & 1 & 1 & 1 & 0 & 0 & 0 & 0\\1 & 1 & 1 & 0 & 0 & 0 & 0 & 1 & 1 & 1 & 0 & 1 & 0 & 0 & 0 & 0\\0 & 1 & 1 & 1 & 1 & 0 & 0 & 0 & 1 & 0 & 1 & 1 & 0 & 0 & 0 & 0\\0 & 0 & 1 & 1 & 0 & 1 & 0 & 1 & 1 & 1 & 1 & 0 & 0 & 0 & 0 & 0\\1 & 0 & 1 & 0 & 1 & 0 & 1 & 1 & 1 & 0 & 1 & 0 & 0 & 0 & 0 & 0\\0 & 0 & 0 & 1 & 0 & 0 & 1 & 1 & 0 & 0 & 0 & 1 & 0 & 0 & 0 & 0\\1 & 0 & 0 & 0 & 1 & 1 & 0 & 0 & 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0\\0 & 1 & 0 & 1 & 1 & 1 & 0 & 1 & 0 & 1 & 0 & 1 & 0 & 0 & 0 & 0\\0 & 1 & 1 & 1 & 1 & 0 & 1 & 0 & 1 & 1 & 0 & 0 & 0 & 0 & 0 & 0\\1 & 1 & 0 & 1 & 0 & 0 & 0 & 1 & 1 & 1 & 1 & 0 & 0 & 0 & 0 & 0\\1 & 0 & 1 & 1 & 1 & 0 & 0 & 0 & 0 & 1 & 1 & 1 & 0 & 0 & 0 & 0\\1 & 1 & 1 & 0 & 0 & 1 & 0 & 1 & 0 & 0 & 1 & 1 & 0 & 0 & 0 & 0\\0 & 1 & 1 & 1 & 1 & 0 & 1 & 0 & 1 & 1 & 0 & 0 & 1 & 0 & 0 & 0\\1 & 1 & 0 & 1 & 0 & 0 & 0 & 1 & 1 & 1 & 1 & 0 & 0 & 1 & 0 & 0\\1 & 0 & 1 & 1 & 1 & 0 & 0 & 0 & 0 & 1 & 1 & 1 & 0 & 0 & 1 & 0\\1 & 1 & 1 & 0 & 0 & 1 & 0 & 1 & 0 & 0 & 1 & 1 & 0 & 0 & 0 & 1\end{array}\right]\]For 5x5 puzzles:
\[C_5 = \displaystyle \left[\begin{array}{ccccccccccccccccccccccccc}0 & 1 & 1 & 1 & 0 & 0 & 0 & 1 & 0 & 1 & 0 & 0 & 0 & 1 & 1 & 0 & 0 & 0 & 0 & 1 & 0 & 0 & 0 & 0 & 0\\1 & 1 & 0 & 1 & 1 & 0 & 1 & 0 & 0 & 0 & 0 & 0 & 1 & 1 & 1 & 0 & 0 & 0 & 1 & 0 & 0 & 0 & 0 & 0 & 0\\1 & 0 & 1 & 1 & 1 & 1 & 0 & 1 & 1 & 0 & 0 & 0 & 1 & 1 & 0 & 1 & 1 & 1 & 1 & 1 & 0 & 1 & 0 & 0 & 0\\1 & 1 & 1 & 0 & 0 & 0 & 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 1 & 0 & 0 & 0 & 1 & 1 & 1 & 0 & 0\\0 & 1 & 1 & 0 & 1 & 1 & 0 & 0 & 0 & 0 & 1 & 0 & 1 & 0 & 1 & 0 & 0 & 1 & 0 & 1 & 1 & 1 & 0 & 0 & 0\\0 & 0 & 1 & 0 & 1 & 0 & 1 & 1 & 0 & 1 & 0 & 0 & 1 & 0 & 0 & 0 & 0 & 0 & 1 & 1 & 0 & 0 & 0 & 0 & 0\\0 & 1 & 0 & 1 & 0 & 1 & 1 & 0 & 1 & 1 & 0 & 0 & 0 & 1 & 0 & 1 & 1 & 1 & 0 & 0 & 0 & 1 & 0 & 0 & 0\\1 & 0 & 1 & 0 & 0 & 1 & 0 & 1 & 1 & 0 & 0 & 0 & 0 & 0 & 1 & 1 & 0 & 1 & 0 & 1 & 1 & 0 & 1 & 0 & 0\\0 & 0 & 1 & 0 & 0 & 0 & 1 & 1 & 1 & 0 & 1 & 0 & 0 & 1 & 1 & 1 & 0 & 0 & 1 & 0 & 0 & 1 & 1 & 0 & 0\\1 & 0 & 0 & 0 & 0 & 1 & 1 & 0 & 0 & 0 & 1 & 0 & 1 & 0 & 1 & 0 & 1 & 1 & 0 & 1 & 0 & 0 & 1 & 0 & 0\\0 & 0 & 0 & 0 & 1 & 0 & 0 & 0 & 1 & 1 & 0 & 0 & 1 & 0 & 1 & 1 & 1 & 1 & 1 & 0 & 0 & 1 & 0 & 0 & 0\\0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 1 & 0 & 0 & 0 & 1 & 1 & 1 & 0 & 0\\0 & 1 & 1 & 0 & 1 & 1 & 0 & 0 & 0 & 1 & 1 & 0 & 1 & 1 & 0 & 0 & 0 & 1 & 0 & 0 & 1 & 1 & 0 & 0 & 0\\1 & 1 & 1 & 0 & 0 & 0 & 1 & 0 & 1 & 0 & 0 & 0 & 1 & 1 & 1 & 0 & 0 & 0 & 1 & 0 & 0 & 0 & 0 & 0 & 0\\1 & 1 & 0 & 0 & 1 & 0 & 0 & 1 & 1 & 1 & 1 & 0 & 0 & 1 & 1 & 1 & 1 & 0 & 1 & 0 & 1 & 0 & 0 & 0 & 0\\0 & 0 & 1 & 0 & 0 & 0 & 1 & 1 & 1 & 0 & 1 & 0 & 0 & 0 & 1 & 1 & 0 & 1 & 0 & 1 & 1 & 0 & 1 & 0 & 0\\0 & 0 & 1 & 1 & 0 & 0 & 1 & 0 & 0 & 1 & 1 & 1 & 0 & 0 & 1 & 0 & 1 & 1 & 1 & 0 & 0 & 0 & 1 & 0 & 0\\0 & 0 & 1 & 0 & 1 & 0 & 1 & 1 & 0 & 1 & 1 & 0 & 1 & 0 & 0 & 1 & 1 & 0 & 1 & 1 & 1 & 0 & 0 & 0 & 0\\0 & 1 & 1 & 0 & 0 & 1 & 0 & 0 & 1 & 0 & 1 & 0 & 0 & 1 & 1 & 0 & 1 & 1 & 1 & 0 & 0 & 0 & 1 & 0 & 0\\1 & 0 & 1 & 0 & 1 & 1 & 0 & 1 & 0 & 1 & 0 & 0 & 0 & 0 & 0 & 1 & 0 & 1 & 0 & 1 & 1 & 0 & 1 & 0 & 0\\0 & 0 & 0 & 1 & 1 & 0 & 0 & 1 & 0 & 0 & 0 & 1 & 1 & 0 & 1 & 1 & 0 & 1 & 0 & 1 & 1 & 1 & 0 & 0 & 0\\0 & 0 & 1 & 1 & 1 & 0 & 1 & 0 & 1 & 0 & 1 & 1 & 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 1 & 1 & 1 & 0 & 0\\0 & 0 & 0 & 1 & 0 & 0 & 0 & 1 & 1 & 1 & 0 & 1 & 0 & 0 & 0 & 1 & 1 & 0 & 1 & 1 & 0 & 1 & 0 & 0 & 0\\0 & 1 & 1 & 1 & 0 & 1 & 0 & 1 & 0 & 1 & 1 & 1 & 0 & 1 & 1 & 1 & 0 & 1 & 0 & 1 & 0 & 1 & 1 & 1 & 0\\1 & 0 & 1 & 0 & 1 & 1 & 0 & 1 & 0 & 1 & 0 & 0 & 0 & 0 & 0 & 1 & 0 & 1 & 0 & 1 & 1 & 0 & 1 & 0 & 1\end{array}\right]\]And given a solvable board its easy to confirm that \(Cb\) gives us the squares to click
A Naive Solving Algorithm
Matrices aside, one way that I noticed I could solve the 4x4 for grid was to start by clicking squares on the 3rd row until the 4th row was solved, and then click the 2nd row until the 3rd row is solved, and then click the 1st row until the second row is solved. It’s pretty clear that after these steps rows 2-4 are solved but what I noticed was that row 1 would also end up solved!
heres an example

I was curious if we can prove if this algorithm always works.
This comes down to proving that if \(b\) is solvable, and the last 8 entries of \(b\) are 0,
then \(C_4 b\) has 0’s for the last 12 entries.
Since \(b\) is solvable by assumpution \(C_4 b\) has 0s for the last 4 entries.
lets say \(x\) is the first 8 elements of \(b\) and lets say \(D_4\) is \(C_4[13:16,1:8]\), \(D_3 = C_4[9:12,1:8]\) and \(D_2 = C_4[5:8,1:8]\)
\[D_4 = \displaystyle \left[\begin{matrix}0 & 1 & 1 & 1 & 1 & 0 & 1 & 0\\1 & 1 & 0 & 1 & 0 & 0 & 0 & 1\\1 & 0 & 1 & 1 & 1 & 0 & 0 & 0\\1 & 1 & 1 & 0 & 0 & 1 & 0 & 1\end{matrix}\right]\] \[D_3 = \displaystyle \left[\begin{matrix}0 & 1 & 1 & 1 & 1 & 0 & 1 & 0\\1 & 1 & 0 & 1 & 0 & 0 & 0 & 1\\1 & 0 & 1 & 1 & 1 & 0 & 0 & 0\\1 & 1 & 1 & 0 & 0 & 1 & 0 & 1\end{matrix}\right]\] \[D_2 = \displaystyle \left[\begin{matrix}1 & 0 & 1 & 0 & 1 & 0 & 1 & 1\\0 & 0 & 0 & 1 & 0 & 0 & 1 & 1\\1 & 0 & 0 & 0 & 1 & 1 & 0 & 0\\0 & 1 & 0 & 1 & 1 & 1 & 0 & 1\end{matrix}\right]\]We know that \(D_4 x = 0\) since \(b\) is solvable. Since \(D_3 = D_4\) then \(D_3 x = 0\)
Now we just need to show \(D_2 x = 0\)
We can look at the solutions (in reduced matrix form) of \(D_4x = 0\)
\[[D_4'|0] = \displaystyle \left[\begin{matrix}1 & 0 & 0 & 0 & 1 & 1 & 0 & 0\\0 & 1 & 0 & 0 & 1 & 1 & 1 & 0\\0 & 0 & 1 & 0 & 0 & 1 & 1 & 1\\0 & 0 & 0 & 1 & 0 & 0 & 1 & 1\end{matrix} \left| \displaystyle \begin{matrix}0\\0\\0\\0\end{matrix} \, \right. \right]\]and \(D_2 x = 0\)
\[[D_2'|0] = \displaystyle \left[\begin{matrix}1 & 0 & 0 & 0 & 1 & 1 & 0 & 0\\0 & 1 & 0 & 0 & 1 & 1 & 1 & 0\\0 & 0 & 1 & 0 & 0 & 1 & 1 & 1\\0 & 0 & 0 & 1 & 0 & 0 & 1 & 1\end{matrix} \left| \displaystyle \begin{matrix}0\\0\\0\\0\end{matrix} \, \right. \right]\]which have the same set of solutions! Which means once we have naively cleared the 4th and 3rd row, the only tiles left to click are in row 1.
The tiles to click in row 1 need to be exactly the ones that are right above the black squares in row 2 (tiles in row 1 affect exactly 1 tile in row 2 so we are forced to click only those).
This proves that this algorithm should always work on solvable 4x4 boards!
Conclusion
Expressing the changes in tiles as a linear transformation of clicks (\(\mod(2)\)) gives us a useful tool to formally reason about the Tile puzzle. We both can solve the puzzle, analyze the number of solutions of the puzzle, and express intuitive solving algorithm using this framework.
There’s probabaly a lot of other stuff we can deduce using these matrices but this seems like enough for now.