Slay the Spire, the Defect, and Turing Completeness
February 3rd , 2025 by Rohan Rao
Slay the Spire, The Defect, and Turing Completeness
Slay the Spire is a very popular roguelike deckbuilding game in which a player plays as one of 4 characters to progress through a dungeon and defeat bosses and monsters along the way. Having played this character before will make the rest of this more understandable but I’ll highlight the relevant mechanics we care about.
Battles in slay the spire are turn based. On the players turn, they play a character and play cards that deal damage to the enemy, block damage from the enemy, or grant special effects. Next the enemy takes a turn where the enemy takes actions like dealing damage, blocking, or other special effects. Then it’s the player’s turn again.
The character that matters for this post is the Defect. The Defect’s mechanic is that it maintains a queue of orbs (where each orb grants some block or damage) and has special available cards that can be added to its deck that manipulate these orbs. (Below is an image of the defect with lightning and frost orbs).

Orbs trigger their effects Passive-ly (which trigger for Lightning and Frost at the end of the players turn) and through cards that Evoke them. The Evoke effect is usually stronger than the Passive but it will pop the front orb out of the Defect’s queue. Focus is a buff/debuff that the Defect can receive that will modify the Passive/Evoke effect of an orb. For example \(+1\) Focus will make Lightning effects deal 1 more damage and Frost block one more.
| Orb Type | Passive Effect | Evoke Effect |
|---|---|---|
| Lightning | Deal 3 Damage to a Random Enemy | Deal 8 Damage to a Random Enemy |
| Frost | Block 2 | Block 5 |
The way that orbs were being added and removed from the queue reminded me of a popular object of study in computer science - a turing machine. Additionally thematically the Defect is a robot of sorts so that also reminded me of a Turing machine.

This lead me to the following question
Is the Battle Outcome Decideable?
Lets pretend we have a set of all reasonable slay the spire enemies \(\mathbb{M}\) of which
\[\{Lagavulin, Reptomancer, Cultist, ...\} \subset \mathbb{M}\]Given a deterministic game state is there an algorithm that can determine if the player is going to lose against a \(monster \in \mathbb{M}\) (for all monsters)?
For some monsters this is certainly true. For some monsters you can just compute out all the possibilities of the game tree (since there is no randomness) and see if optimal play results in a win or loss.
I’ll show though with some minor tweaks to the rules of the game there are some \(m \in \mathbb{M}\) such that no such algorithm can exist.
The main tweak to the defect is we are going to remove the cap of 10 orb slots that the defect has.
CT Language
As an aside that will be useful
CT is a turing-complete programming language. The language manipulates a data string and the program stops running if the data string runs out of bits. The program loops through a set of commands (starting over once it reaches the last command)
| Command | Operation |
|---|---|
| 0 | pop front bit of data string |
| 1 | if front bit is 1 append 1 to the end of the data string |
| 2 | if front bit is 1 append 0 to the end of the data string |
So for example lets say we run program
0102 on datastring 110011
heres the runtime of the program (first line is initial data string and each following line is the result of running the relevant operation on the data string)
Run instruction 0 on 110011
Run instruction 1 on 10011
Run instruction 0 on 100111
Run instruction 2 on 00111
Run instruction 0 on 00111
Run instruction 1 on 0111
Run instruction 0 on 0111
Run instruction 2 on 111
Run instruction 0 on 1110
Run instruction 1 on 110
Run instruction 0 on 1101
Run instruction 2 on 101
Run instruction 0 on 1010
Run instruction 1 on 010
Run instruction 0 on 010
Run instruction 2 on 10
Run instruction 0 on 100
Run instruction 1 on 00
Run instruction 0 on 00
Run instruction 2 on 0
Run instruction 0 on 0
HALT
here’s a program that loops forever
program = "1" data = "1"
Run instruction 1 on 1
Run instruction 1 on 11
Run instruction 1 on 111
Run instruction 1 on 1111
...
Since this language is turing-complete, there’s no computer algorithm that takes a program and data as input and outputs whether the program reaches the halt state when run on this data (this is a well known result that the halting problem is undecidable).
We’ll draw a correspondence between an algorithm that determines whether a CT program halts on a given input and an algorithm that can determine, for any enemy, whether the Defect will lose a game state.
Encoding a CT Program in a Slay the Spire Enemy
Its not yet clear what the elements of \(\mathbb{M}\) are. We’ve seen examples of enemies in Slay the Spire but our argument requires a more general definition of a slay the spire enemy.
The sketch of the idea here is that for every CT program we’ll find some corresponding enemy in \(\mathbb{M}\) such that when battling this enemy as the Defect the player is forced to take certain moves and will lose only if the program halts.
This requires us to define some conditions of membership to \(\mathbb{M}\). We’ll come up with a “blueprint” for an enemy that exists in \(\mathbb{M}\). Not every slay the spire enemy needs to follow this but enemies that follow this blueprint can be considered to be members of \(\mathbb{M}\).
The enemies we’ll consider will loop between a sequence of moves, and moves will be composed of multiple actions
The actions we’ll allow enemies to do on their turn are in the table below. I’ll cite what sort of existing enemy in slay the spire does an action of this sort (or indicate if they are new).
| Action | Precedent | Effect | icon |
|---|---|---|---|
| Block \(X\) | Many Enemies | Applies \(X\) block | |
| Attack \(X\) | Many Enemies | Deal \(X\) damage | |
| Summon Minions | Gremlin Leader, Reptomancer | Explained Below | |
| Add Void | Awakened One, Corrupt Heart | Add Void to player discard | |
| Anger | Angry Gremlin | Each damage dealt from an attack card to enemy increases enemy strength |
|
| malleable | snake plant | Each damage dealt to enemy from attack causes enemy to gain block | |
| peace | NEW | skills played increases enemy dexterity |
|
| split | slime boss | when reduced to \(\leq 1/2\) health, cancel actions and split into two slimes with hp maching current hp | |
| shifting | transient | damage dealt to enemy decreases enemy’s attack strength this turn |
|
| regenerate | the awakened one | heal at end of turn |
strength and dexterity are additive adjusts to attack and block that enemies can keep track of.
The new buff I added was peace ability which is just the symmetric dexterity buffs to the enraged strength buffs. I personally think this is a natural extension of the actions that exist in Slay the Spire so I don’t feel like it’s too much of a departure from the game to introduce these to the enemy action set.
Void is a special type of card

One of the actions I’ll elaborate on is Summon Minions. A minion is a secondary enemy that’s summoned that performs moves alongside the main enemy (and it flees if the main enemy dies.
In the below construction I’ll assume that Minion’s stats can be a function of the main enemy’s strength + dexterity. Although this doesn’t explicitly happen, I think its permissable because the main enemy can buff its minions (Gremlin Leader can block for the minions and raise their strength). But it’s worth noting that this is a bit more flexible than the examples seen in the game.
Here are some extra things minions ![]() can do
can do
| Action | Precedent | Effect | |
|---|---|---|---|
| fading | dagger | will die at end of turn | |
| buff main enemy | increase strength or dexterity of main enemy |
For the purposes of our construction we’ll define a few moves that the enemy can do (over 2 turns) that will be useful for our construction.
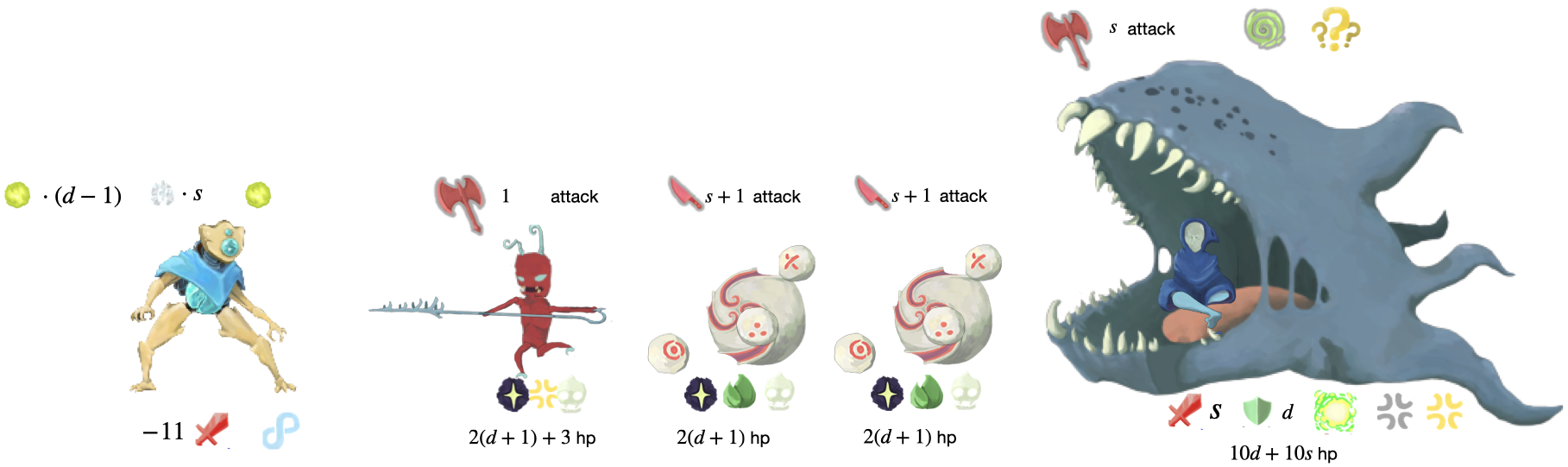
Lets construct an enemy (which graphically looks like)

Let’s say an enemy has strength \(s\) and dexterity \(d\), and starts each turn with \(10s\) block. We’ll also say the enemy regenerates \(10s\) each turn (so is unkillable).
| Composite Move Number | Name | Turn 1 | Turn 2 | Turn 3 |
|---|---|---|---|---|
| 0 | Call Slime | Summon Support Slime |
\(d \rightarrow d - 1\) | add Void status to player discard |
| \(s \rightarrow s - 1\) | ||||
add Void status to player discard |
||||
| 1 | Hire Assasins | starts turn angry |
add Void status to player discard |
N/A |
Summon minion attacking for \(s + 2\) with \(2(d + 1) + 3\) HP with anger and fading |
Summon Auditor | |||
| 2 | Hire Brawlers | starts turn angry and attacking for \(s\) with peace |
add Void status to player discard |
N/A |
Summon minion attacking for \(s + 1\) with \(2(d + 1)\) HP with 2 malleable and fading |
Summon Auditor | |||
Summon minion attacking for \(s + 1\) with \(2(d + 1)\) HP with 2 malleable and fading |
||||
Summon minion attacking for \(1\) with \(2(d + 1) + 3\) HP with anger and fading |
and some details about Support Slime. The slime will be attacking for \(s + 4\), will have hp of \(4d + 14\), will increase dexterity of the main enemy by 1, and die at the end of its turn. It however will split/get interrupted if brought to half health (like other slimes). It will split into two slimes where one of the slimes will raise the main enemy’s strength by 1 and have fadingf. Here’s a visual:
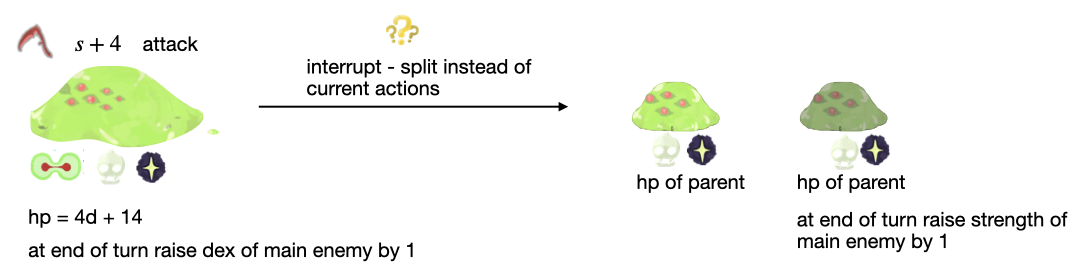
The Auditor is
| Auditor |
|---|
| minion atttacking with \(s + 2d + 1\) with HP of \(10d + 10s\) |
| has shifting |
| has fading |
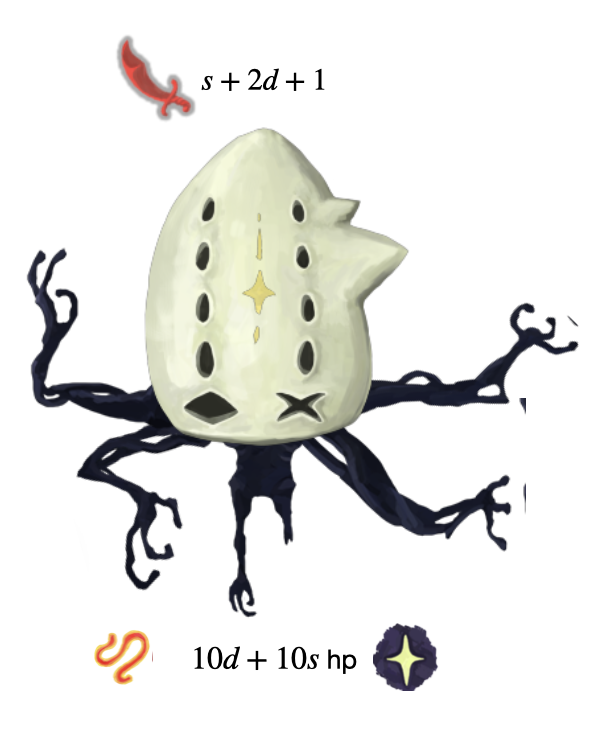
The enemies we’ll consider are ones that loop between moves from this moveset.
For example, if we have an enemy that runs 1120 it will Hire Assasins on turns 1-2, then Hire Assasins again on turns 3-4, then Hire Brawlers on turn 5-6, then Call Slime on turns 7-9. Then it would start over and Hire Assasins on turns 10-11.
Later I’ll show that an enemy that follows moveset 1120 encodes the program 1120.
Encoding the Data String In the Defect State
Now that I’ve claimed that we can encode the program in a slay the spire enemy, we need to encode the data string in the Defect’s Game State.
We’ll initialize the orbs with Frost for every 1 in the data string and Lightning for every 0.
If we have a data string with 1001 we’ll (starting from the front slot) have Frost, Lightning, Lightning, Frost. If we don’t have enough orb slots we’ll pretend we have played enough Capacitor cards to allow it.
We’ll also start with Loop played, Electrodynamics played, and 2 Fasting played (this is possible bc of Prismatic Shard).
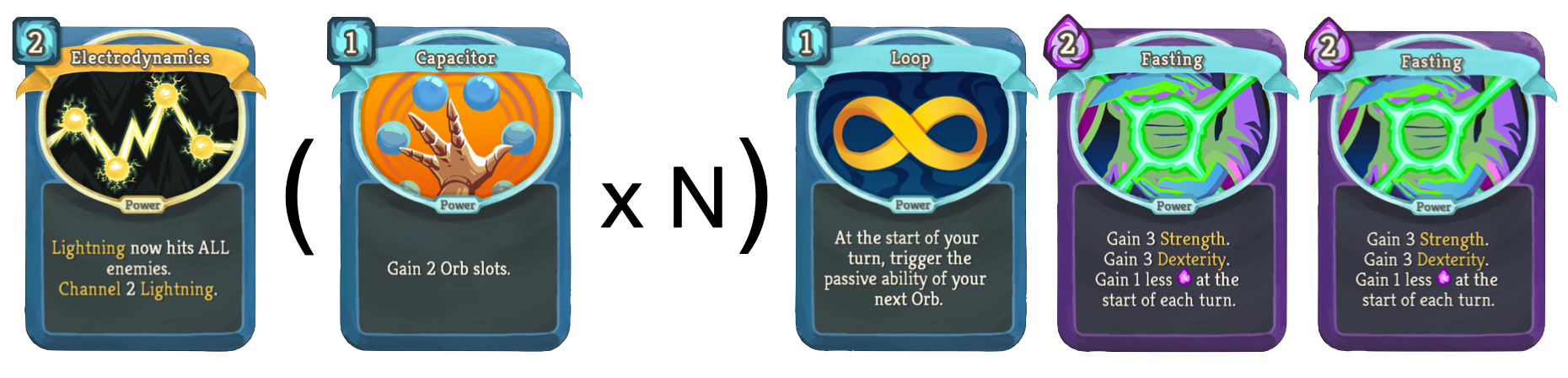
We’ll start with Inserter in the relic slots, and also have Prismatic Shard

For cards in deck we’ll only have 4 cards (so every turn we draw the same 4 cards). We’ll have
Zap, Cold Snap, Quick Slash, Multicast

For buffs/debuffs, lets initialize \(-11\) strength and \(-1\) focus. (this will keep numbers nicer). Notably this means Lightning does \(2\) passive and \(7\) evoke damage. Frost blocks \(1\) passive and \(4\) when evoked. Quick Slash only does \(3\) damage (\(+6\) strength from Fasting but \(-11\) strength debuffed applied to a base damage of \(8\))
Finally, in our game state the Defect has 1 HP left.
Finishing The Construction
Lets make the previous two sections a little more precise by defining the mapping between a CT Program and Data String into a slay the spire game state.
Lets start with encoding our Data String in the Defect starting state as described in our previous section. Then we initialize our Enemy with strength equal to the number of Frost Orbs that the Defect is initialized with and dexterity equal to the number of Lightning Orbs that the Defect is initialized with. Then we give the enemy the moveset descibed in prior section based on the Program we are trying to encode. It’s the enemy’s turn to start with in this game state.
Then determining if the Defect loses in this state is the same as determining if the Program halts on the Data. We’ll argue this in the next section.
Why does our program and data encoding work?
With the above encoding of a program and data into a game state, we just need to show that the progression of the battle follows the way that the program manipulates the data string. For us to do this we’ll show that the enemy moves force the player to play certain cards. And at the end of the players turns the orb configuration matches the data string after running the CT instruction.
Now when an enemy takes any of these moves it will force actions on our end to avoid losing immediately. Note that since during turn 2 of every composite enemy move the player has no energy so can play no cards
| Enemy Move Number | Forced Defect Move 1 | Proof Number | Orb Effect |
|---|---|---|---|
| 0 | evoke front orb | (A) | Remove Front Orb |
| 1 | if front orb is frost then play Cold Snap |
(B) | Add frost to back |
if front orb is lightning then play Quick Slash |
(C) | ||
| 2 | if front orb is frost then play Zap |
(D) | Add lightning to back |
if front orb is lightning then play Quick Slash |
(E) |
We’ll also show the invariant that after each enemy move is over, the strength and dex of the enemy matches the number of frost and lightning orbs respectively. The base case of this is true by construction on initialization so we just need to show that the below moves don’t change that. For all the below we assume this invariant.
We know the defect has enough orb slots for the initial orbs via the Capacitors but since every enemy composite move lasts at least two turns, and leads to the addition of at most 1 orb to the defects orbs, our inserter triggers to keep enough orb slots for us.
It’s clear that if the defect has no orbs left then the defect loses (Loop triggering is a necessary condition to survive each turn). We’ll show that otherwise the defect can always survive another turn if it plays the move in the above table.
(A)
In this situation we are facing \(s + 4\) damage from a minion with \(4d + 14\) hp. We have \(s\) frost orbs and \(d\) lightning orbs. To survive we either need to block \(s + 4\) damage or deal \(2d + 7\) damage to get the enemy to split. We have one energy available so we can play only 1 card.
If our front orb is Lightning:
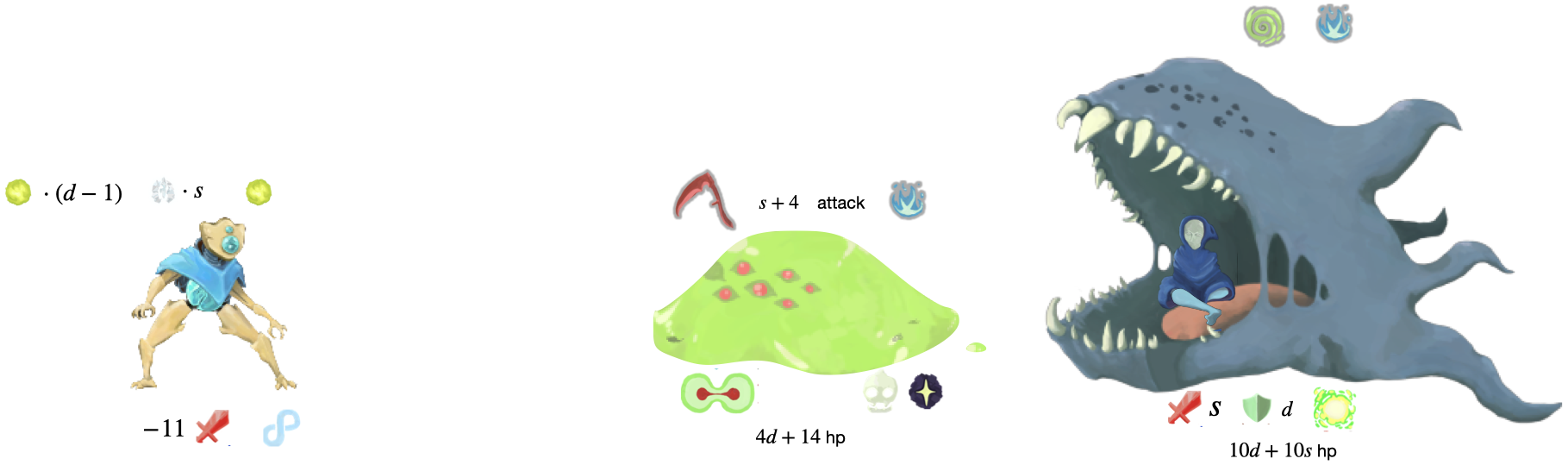
then at the start of our turn we deal 2 damage (through Loop). We’ll block \(s\) damage through our Frost orbs which isn’t enough to save us, so we need to figure out how to deal \(2d + 5\) more damage instead of relying on block.
Playing Quick Slash will let us deal \(3\) more damage and then we’ll do \(2d\) from Lightning orbs passively which doesn’t save us.
Playing Cold Snap will have us deal \(1\) more damage and block \(1\) more which doesn’t save us.
Zap would add a lightning orb so passively we’d do \(2d + 2\) which isn’t enough.
So we need to play Multicast. This will let us deal \(7\) damage immediately and \(2(d-1)\) more at the end of our turn which will trigger a split which will save us for the turn.
On the enemy second turn the slime splits, and we get a Void in our discard, and the enemy debuffs.
On our turn we draw our hand + Void which means we can’t play any cards because we have no energy. The split slime survives because we can’t deal \(2d + 5\) damage.
On the enemy third turn the split slime buffs the main enemy and dies. And we get a Void in our discard.
On our turn we can’t do anything as we have no energy.
so at the end of this turn the enemy is net \(-1\) dex. This means that we are down a Lightning orb and the enemy is down \(1\) dex so the invariant still holds
If our front orb is Frost:
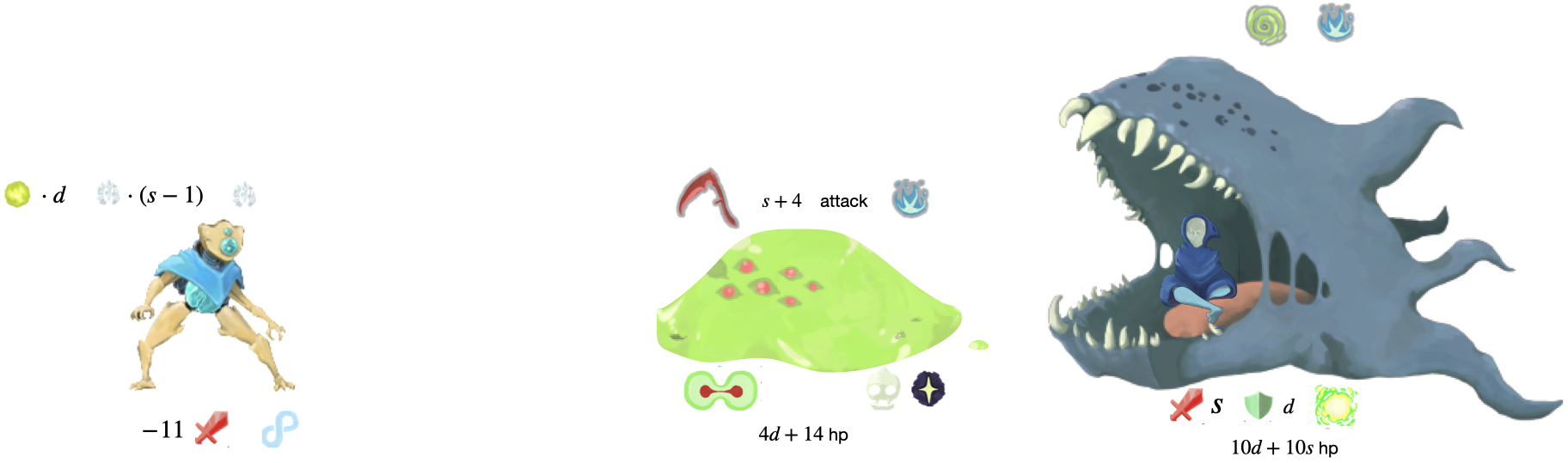
then we have no way to deal \(2d + 7\) damage, so we have to block \(s + 4\). Loop blocks 1 for us, and if we evoke our front orb using Multicast we can block \(4\) immediately and \((s - 1)\) at the end of turn giving us \(s + 4\) total block which saves us.
On the enemy second turn the slime deals damage (which we block), then buffs the main enemy, then dies. We get a Void in our discard. The main enemy debuffs
Our next turn is a no-op because we draw the Void card added into the deck.
The main enemy is net \(-1\) strength. Since we are net \(-1\) Frost then the invariant still holds.
The end result in either case is we are forced to remove our front orb.
(B)
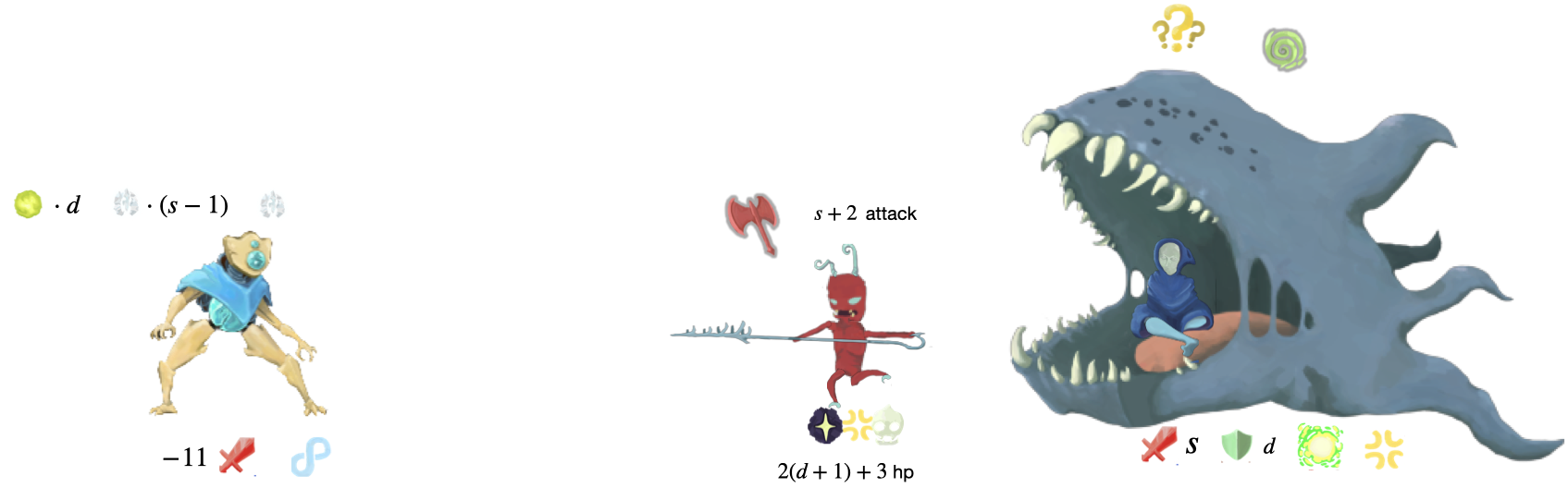
In this situation, we are facing a minion attacking for \(s + 2\) with \(2(d + 1) + 3\) HP. Our front orb is Frost. Loop will start our turn with an extra \(1\) block. No matter what we play we can’t kill this minion so we have to block it. Our options are either to channel a Frost via Cold Snap or play Multicast.
If we play Multicast we’ll die to the auditor next turn (x). So we have to play Cold Snap. This triggers anger so the enemy’s strength goes up by 1. We must target the main enemy otherwise the minion will get too strong and we won’t be able to block
On enemy turn 2 they summon the auditor and give us a Void in our discard.
On our turn we do nothing as we draw the Void. We survive the auditor.
At the end of this sequence we have one more Frost and the enemy has one more Strength
(x) in the case we play Multicast we will be down an orb and the enemy will have one more strength (so now has \(d\) dex and \(s' = s+1\) strength). We can never kill the Auditor. The Auditor is attacking with \(2d + s' + 1 = 2d + s + 2\). Since we are down an orb our attack + block is at most \(2(d + 1) + s - 1 = 2d + s + 1\) which isn’t enough.
(C)
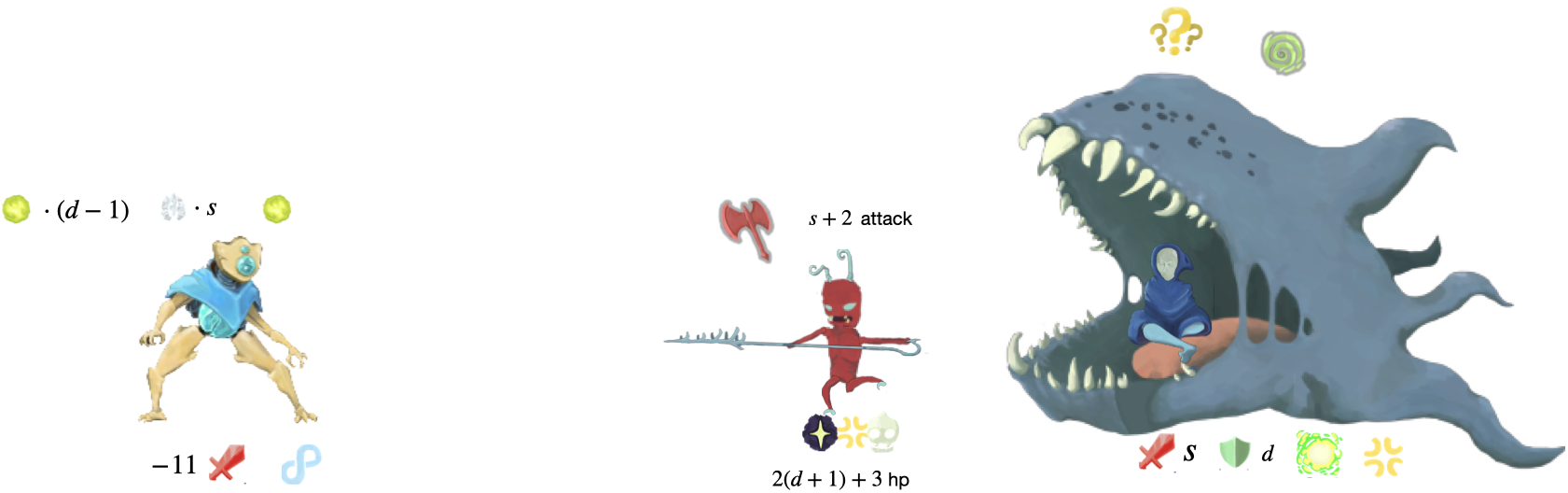
In this situation, we are facing a minion attacking for \(s + 2\) with \(2(d + 1) + 3\) HP. Our front orb is Lightning. Loop will start our turn with an extra \(2\) attack. No matter what we play we can’t block this minion so we have to kill it. Our options are either to Quick Slash - which will kill it, or we can Multicast which also kills it. If we Multicast though we’ll die to the Auditor next turn (x). Cold Snap will only have us block \(s + 1\) total so we still die.
On enemy turn 2 they summon the auditor and give us a Void in our discard.
On our turn we do nothing as we draw the Void. We survive the auditor.
At the end of this sequence we have the same orbs and the enemy has the same Strength and Dexterity.
(x) same argument as in (B)
(D)
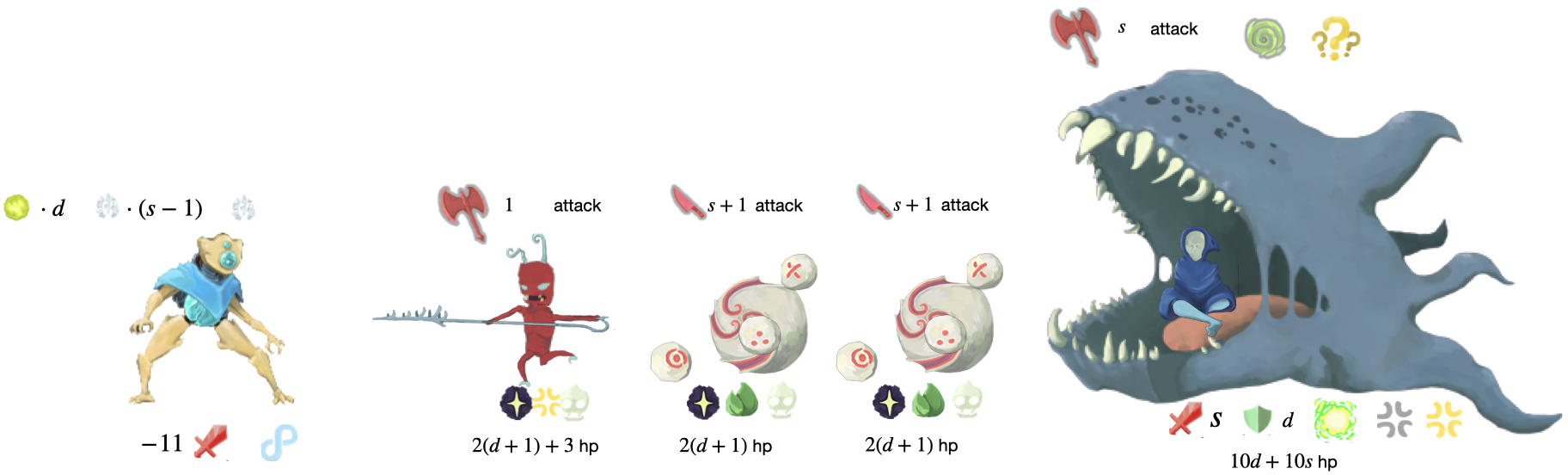
In this situation we are facing three minions. Two are attacking for \(s + 1\) with \(2(d + 1)\) HP. The other is attacking \(1\) with \(2(d + 1) + 3\) HP. The main enemy is attacking for \(s\). We cannot block all of them so our only options are to kill some and block the others. Since our front orb is Frost, Loop blocks 1 to start with and then we can by default block \(s\) more with passive orbs and are dealing \(2d\) damage through Lightning orbs to all enemies. Playing the Quick Slash can kill one of them but two would remain dealing more damage than we can block. Playing Multicast would allow us to instead passively block \(s - 1\) and block 4 via the evoke. This isn’t enough to save us. The only option is to play Zap which will let us deal 2 more damage killing the 2 minions with lower HP and our \(s + 1\) block blocks the damage from the other minion and the main enemy.
Our Lightning orbs go up by 1 and the enemy dex as a result goes up by 1 via peace. We draw a Void next turn and can take no actions. We survive the Auditor.
(E)
In this situation we are facing three minions. Two are attacking for \(s + 1\) with \(2(d + 1)\) HP. The other is attacking \(1\) with \(2(d + 1) + 3\) HP. The main enemy is attacking for \(s\). We cannot block all of them so our only options are to kill some and block the others. Here Loop deals 2 damage to all enemies and by default our lightning orbs will deal \(2d\) passive damage. So the only surviving enemy is the one with the most HP which we can’t block. Zap doesn’t kill it. Multicast would kill it but we wouldn’t survive the Auditor next turn (x). Cold Snap when played will either increase the block of the weaker minions by \(2\) via malleable (making them no longer killable) or increase the attack of the beefy minion or main enemy which all cause us to die. Quick Slash kills and is the only winning situation.
Our orbs and the enemys strength and dex remain unchanged. We draw a Void next turn and can take no actions. We survive the Auditor.
(x) in the case we play Multicast we will be down an orb and the enemy will have one more dex (so now has \(d_1=d + 1\) dex and \(s\) strength). We can never kill the Auditor. The Auditor is attacking with \(2d_1 + s + 1 = 2d + s + 3\). Since we are down an orb our attack + block is at most \(2(d + 1) + s - 1 = 2d + s + 1\) which isn’t enough.
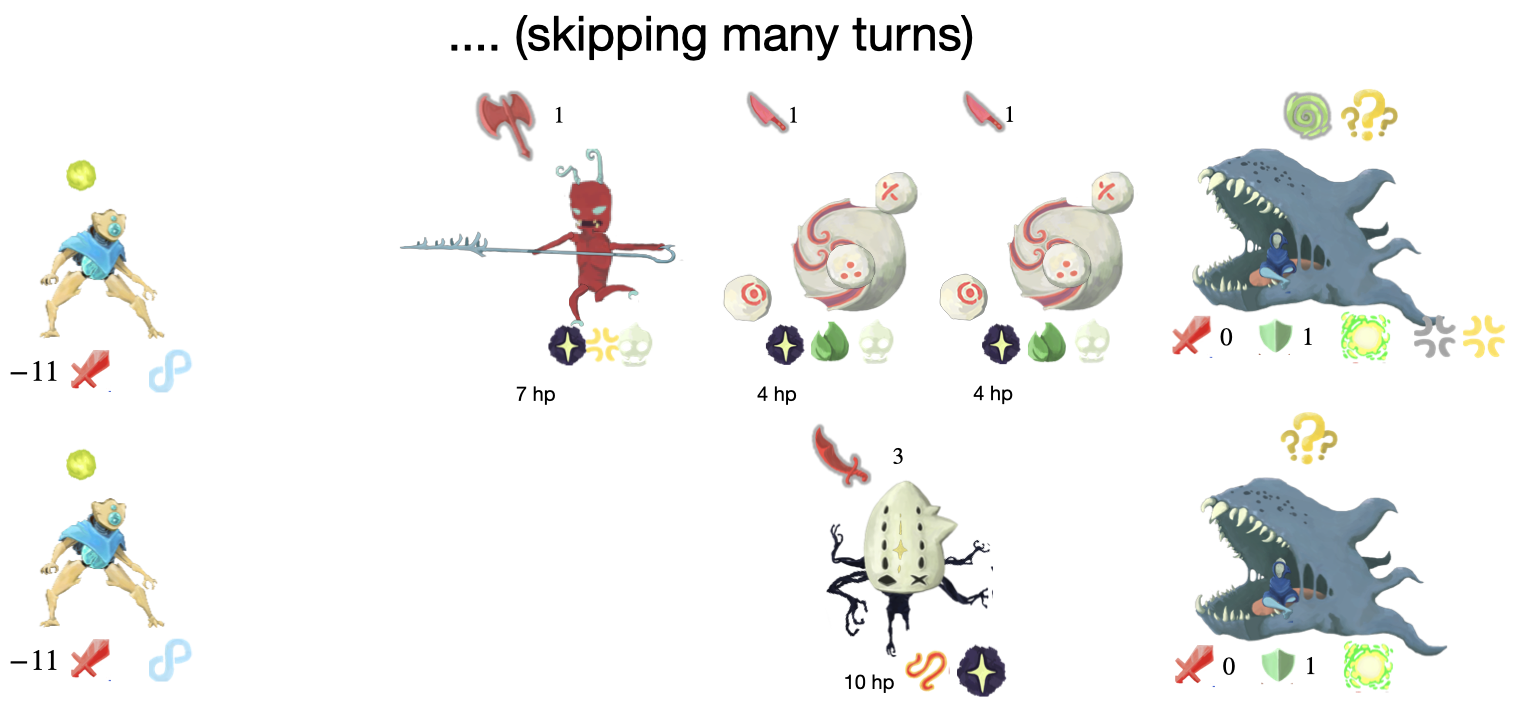
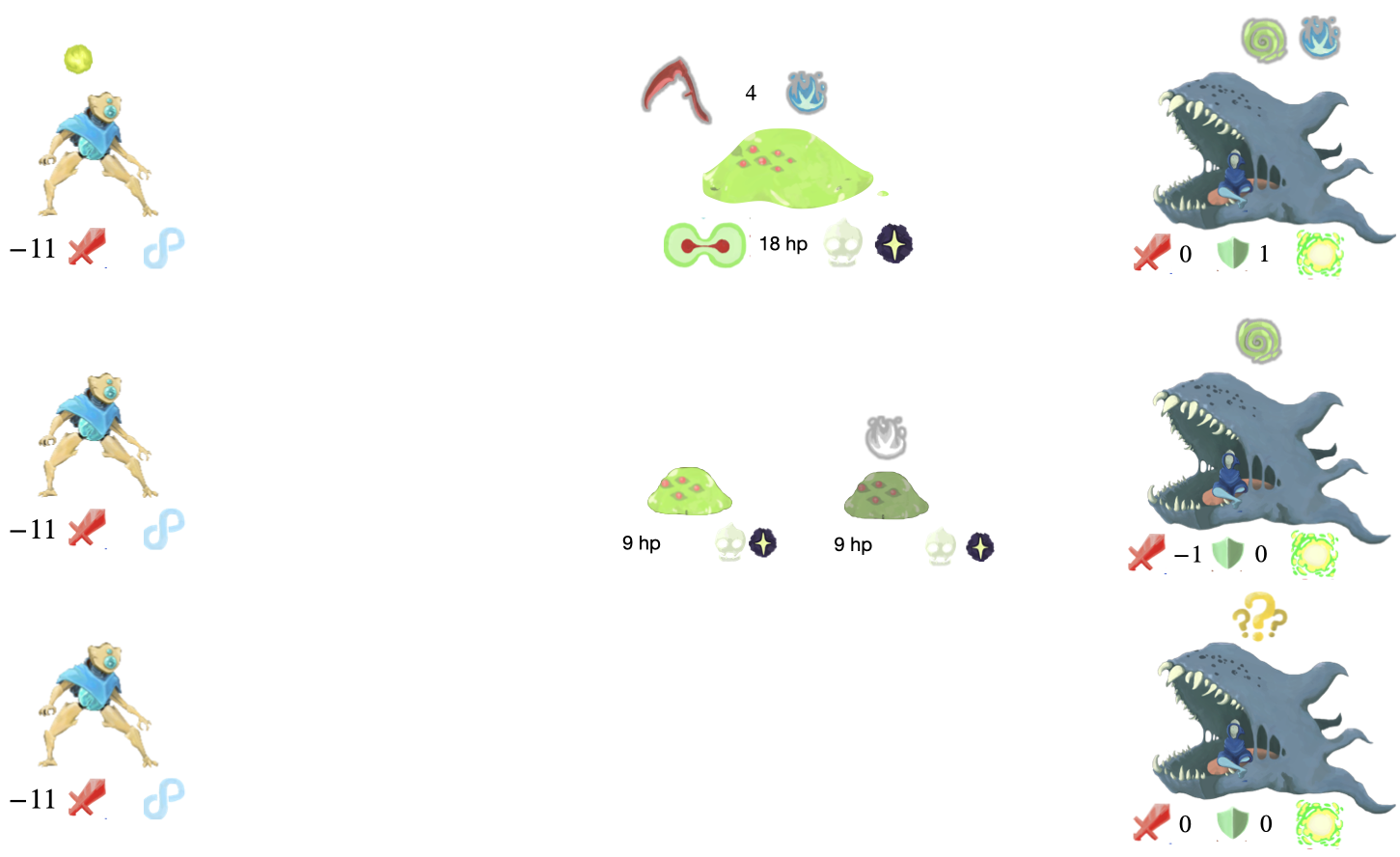
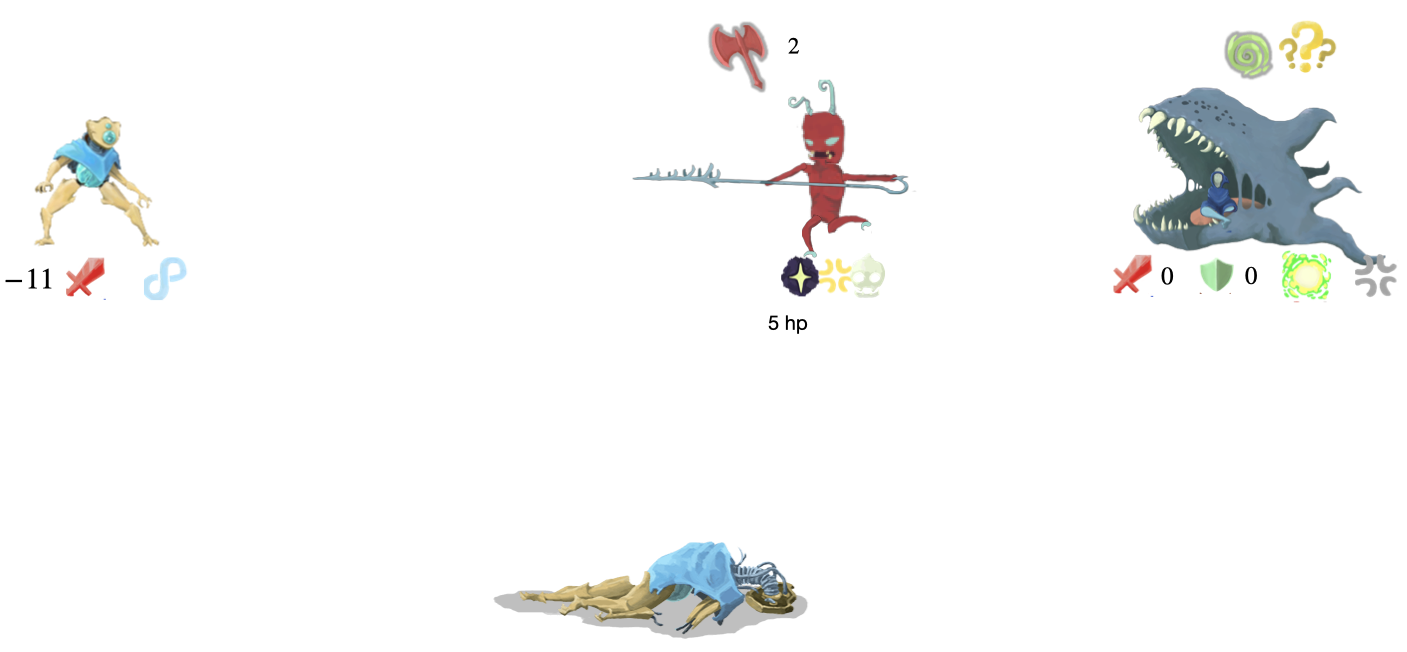
Tracing through an Example Enemy
Lets go through the runtime of encoding the 2010 program run on 101
here’s the CT execution
Run instruction 2 on 101
Run instruction 0 on 1010
Run instruction 1 on 010
Run instruction 0 on 010
Run instruction 2 on 10
Run instruction 0 on 100
Run instruction 1 on 00
Run instruction 0 on 00
Run instruction 2 on 0
Run instruction 0 on 0
And here’s how the fight progression looks (notice the orbs match the data string progression)
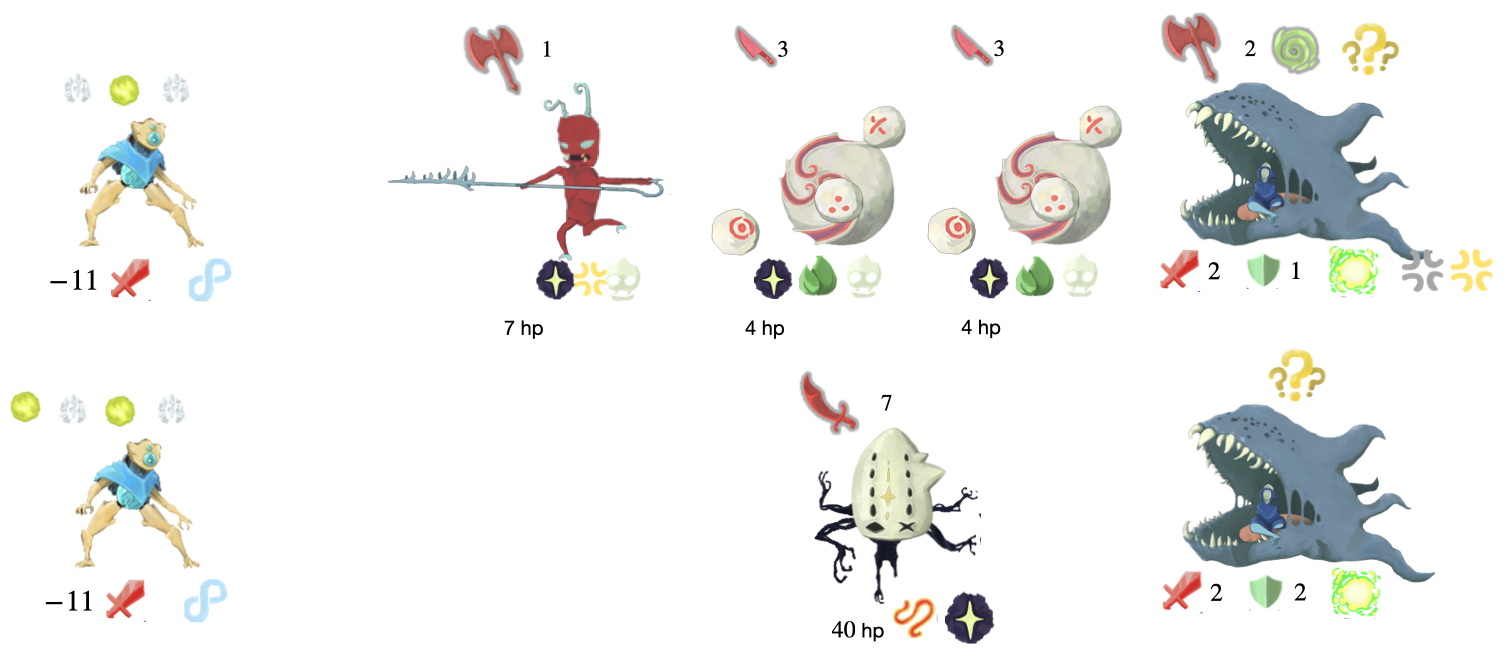

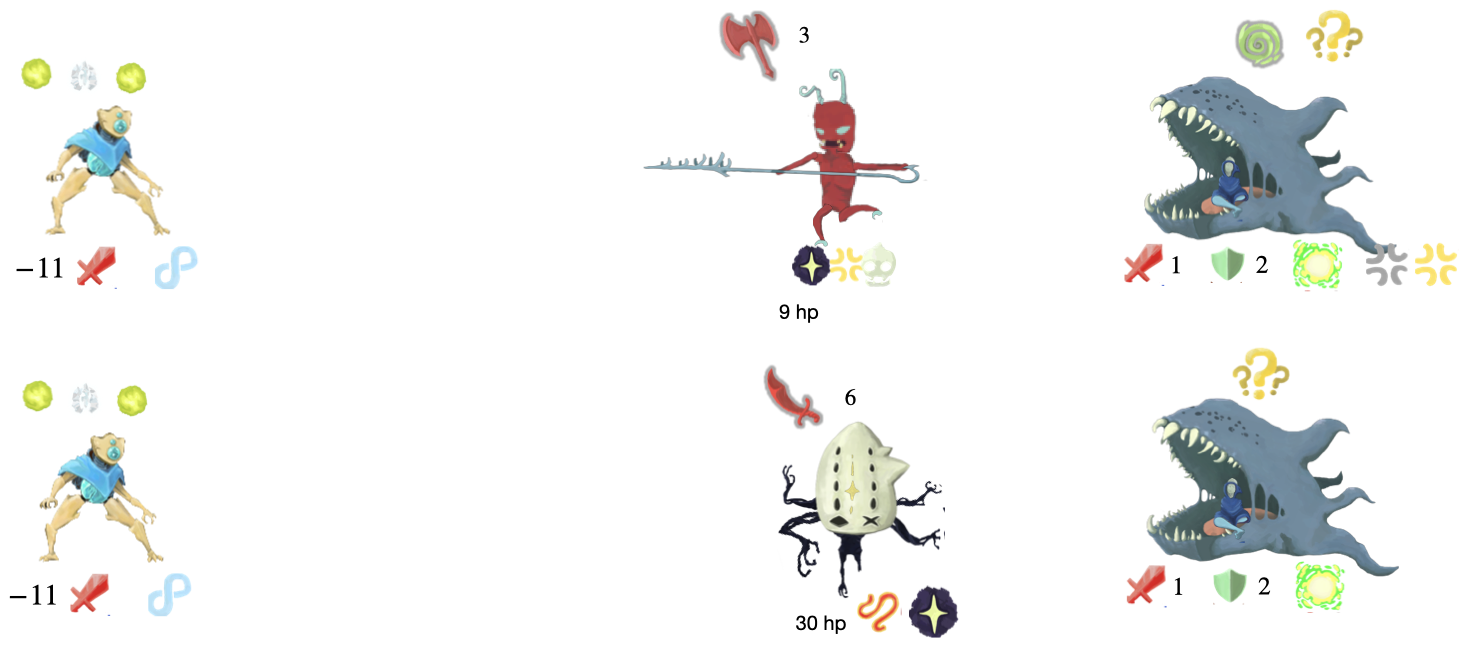
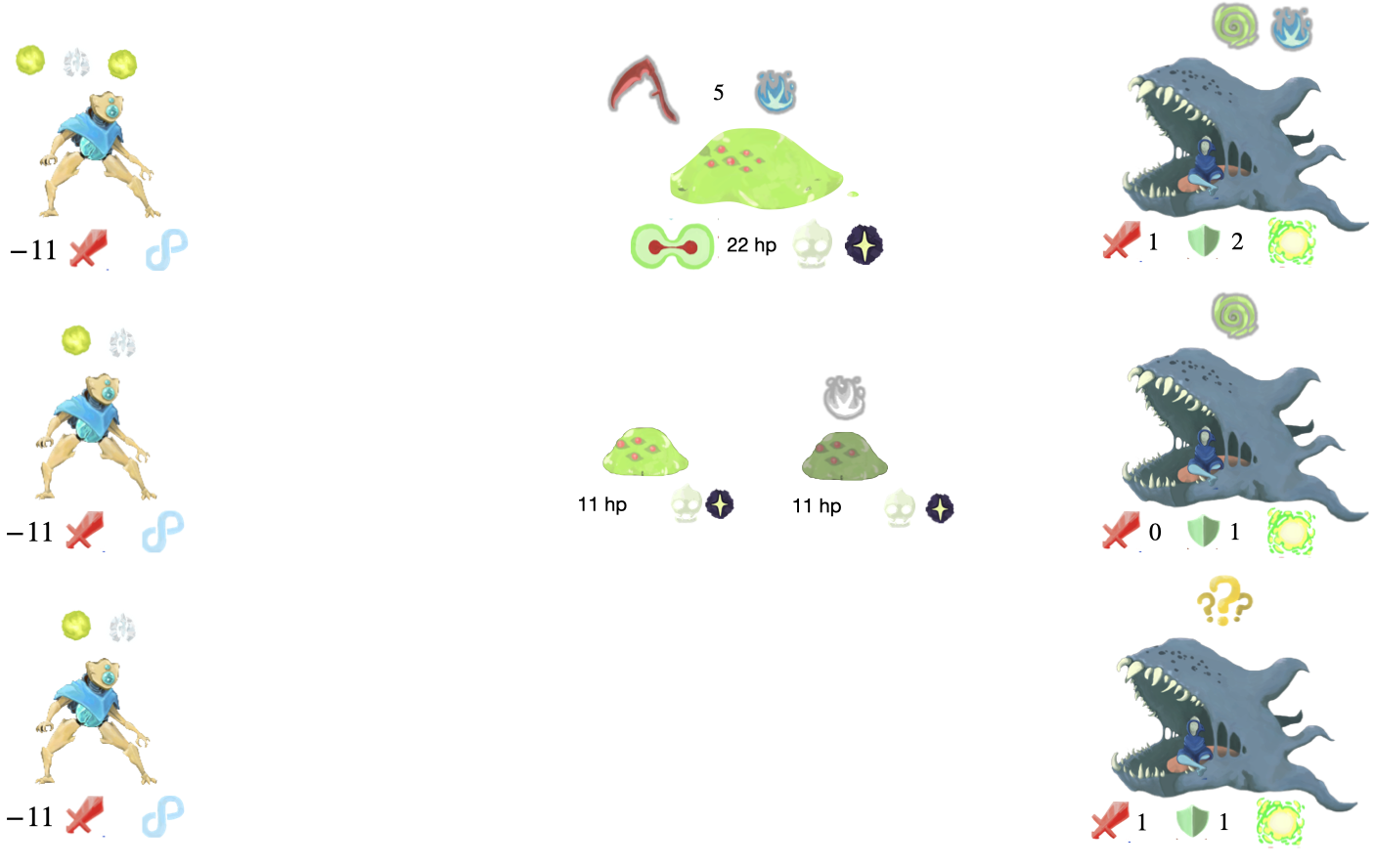
Conclusion
Although its debatable how useful this construction is for any actual slay the spire gameplay, it seems pretty concievable that the defect’s orb mechanics, enemy mechanics, and cards contain significant complexity.
As Slay the Spire 2 is on the horizon, and mods / fan content become more popular it’s probably the case that not all questions about an extended generalized slay the spire-like game would be computationally decidable.
Credits
Thanks to Zhao Li and William Jiao for peer reviewing this!
Slay the Spire: https://www.megacrit.com/games/