How Many Balatro Flushes Should You Expect To Play

May 16th, 2024 by Rohan Rao

Flushes, Hands, and Discards In Balatro

Balatro is a a poker-inspired roguelike deck builder thats fairly popular right now. In the game you have a hand of cards and during each turn you can play a poker hand up to 5 cards (scoring points based on the poker hand that the cards you play make), or discard up to 5 cards. After either action you redraw up to your hand size. You have a certain number of hands and discards available to you.
Here's a little animation that shows an example of a starting hand, then a discard, then playing a hand.

Generally as the game goes on you collect items that improve the way that certain hand types score, and modify the composition of your deck. Eventually decks might specialize to try and play as many hands of the relevant high-scoring type as possible
To simplify things we'll think about a deck which tries to play a lot of flushes

The Main Question

With optimal use of hands and discards, how many flushes should we expect to play? This seemed like an interesting thing to look at because flush builds in Balatro generally are self contained (so it seems more ok to ignore other hand types) and lots of decisions in the game revolve around improving the consistency and number of flushes you are able to play in a round. There are 3 main deck parameters that items in the game can change

(1) hands played (starts at 4)
(2) discards allowed (starts at 3)
(3) hand size (base 8)

Mainly vouchers, stakes, and boss blinds interact with these buut there are also some jokers that modify these aspects of your deck.

Another aspect of your deck that can be modified is the suit of cards in your deck and cards that improve how easy it is to get a flush (smear joker / checker deck, four fingers, tarot cards).

I won't simulate all the possibilities but I'll pick enough to paint a picture

Expected Number of Flushes

if we just think of our hand \(h\) as a vector of size 4 (each entry representing the number of that suit we have, and similarly think of our remaing deck \(r\) and our action \(a\) (either discard or play) as vectors as well (limiting \(0 < \|a\| \leq 5\)).

We can think of \(\mathbb{V}((h,r))\) or value function of that game state as the expected number of flushes being played given optimal play. We can also define a Q-function \(\mathbb{Q}((h,r), a)\) which is the expected number of flushes played in the game if you take action \(a\) at state \((h,r)\). These are related below (assuming we have infinite hands and discards):

\(\mathbb{Q}((h,r), a) = \mathbb{1}_{\max{a} = 5} + \sum_{c} p(c,r)\mathbb{V}((h-a+c, r - c))\)

\(\mathbb{V}((h,r)) = \max_{a}{\mathbb{Q}((h,r),a)}\)

\(p(c,r) = \binom{|r|}{|c|}^{-1}\prod_{i = 1}^4 \binom{r[i]}{c[i]}\)

\(c\) is the vector of cards we draw after discarding or playing. In the above formulation the player picks their vector of cards to play or discard \(a\) and if \(a\) has a flush we’ll play it, otherwise discard it. (unlike the game where you can misclick and ruin a great run). \(p(c,r)\) is the probability of drawing \(c\) from the remaining deck \(r\).

If we have a fixed number of hands and discards unlike the infinite case above we just need to include the plays and discards left in \(\mathbb{V}\) and \(\mathbb{Q}\) which I won’t write out because its verbose (but similar in principle).

Once we have \(\mathbb{V}((h, r))\) for all starting possibilities of \((h,r)\) we can get

\(\mathbb{E}(flushes\_played) = \sum_{s} p(s)\mathbb{V}(s)\)

It’s worth noting that winning a round just requires a player to score enough points and winning in fewer hands gives you a round-end bonus and our version of optimal play functionally ignores this (we just care about the potential number of playable flushes in expectancy).

The expected number of flushes gives us some information about the scoring capacity of our deck (if we went all out how much do we think we can score?), but sometimes we care about consistency (which is more of a claim about the cdf of our distribution of number of flushes). Generally you might want to know the probability that you miss hitting \(n\) flushes. or

\(\mathbb{P}(F < n)\)

Which if we know the expectation we can get a loose bound (Markov style). If \(M = h - F\) where \(h\) is the hands you can play andf \(F\) is the number of flushes you can play. \(M\) is non-negative so

\(\mathbb{P}(F < n) = \mathbb{P}(M \geq h - n) \leq \frac{\mathbb{E}(M)}{h - n} = \frac{h - \mathbb{E}(F)}{h - n}\)

Can also just use the vanilla form for the (pessimistic) other side

\(\mathbb{P}(F \geq n) \leq \frac{\mathbb{E}(F)}{n}\)

Solving the Above Computationally

Generally the above can be solved via dynamic programming (where we cache previous solutions for states and otherwise solve recursively). As written for a given hand size (lets say 8) we have an estimated number of possible states of. Estimated because we might not need to solve all these states (just the ones that we need to compute the value function for all the starting states.

\(\sum_{s} (14-s[0])(14-s[1])(14-s[2])(14-s[3]) = 3,234,330\)

One observation that we can use to further simplify things is that the value function is unchanged if you relabel the colors. In other words if we have a permutation \(\sigma(.)\)

\(\mathbb{V}((\sigma(h), \sigma(r))) = \mathbb{V}((h,r))\)

So we only need to cache one of the permutations which helps a bit - to an estimated upper bound of \(293,042\)

Now we can just simulate.

Hand Sizes

Default Hand Size

By default you start with 8 cards in hand. To start out we'll compute the expected flushes given some different numbers of plays and discards. By default you start out with 4 hands and 3 discards but depending on the deck you are playing with you might start with (4,4) or (5,3). (the red and blue deck). Other decks (black deck) have you start one hands down (but give you another bonus)

Some vouchers or jokers modify these - such as:

Which gives +1 Hand

And also

Which gives +1 Discard

There are a lot of different hands and discards numbers that are feasible throughout the gameplay, so for each scenario I'll pick some to solve. I'll try and pick situations that are more common or interesting in some way but some of the situations I chose to solve for were fairly arbitrary.

The first situation I'll solve is the default 8 card hand size deck. I included also what the expectation would be if you had an infinite number of hands and discards.

png

The above result passes a few basic sanity checks - the marginal hand is better than the marginal discard (but here not by much). And more hands + discards is better.

Paintbrush

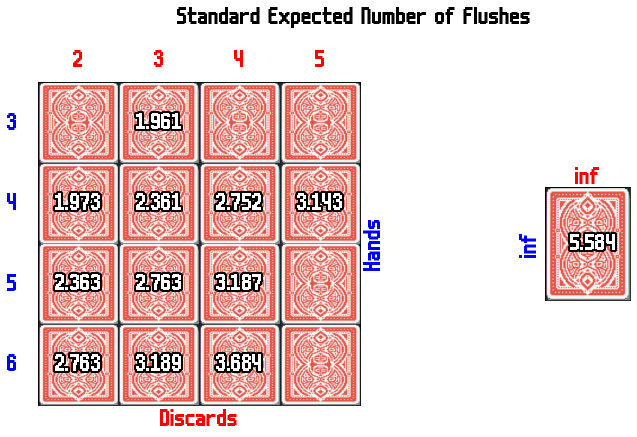
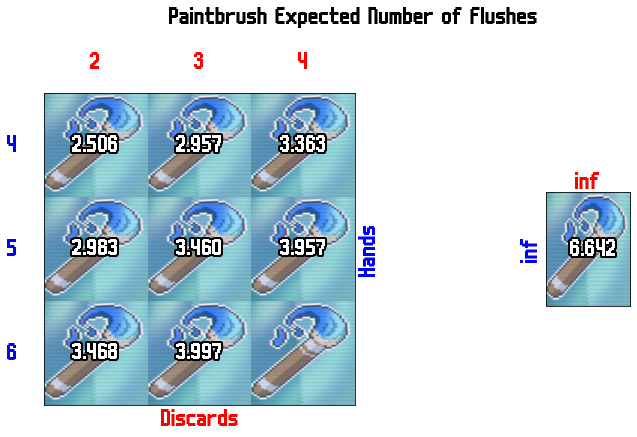
Beyond the 8 card hand size, there are a few vouchers increase your hand size - one example of them is paintbrush which increases hand size by 1 - we'll try a few of the above options but with 9 card hands. (Technically you can stack another voucher or a joker to keep growing hand size but I think these situations are probably less common in practice so I chose not to look at them for the sake of time) (though we could solve for them with the exact same approach).

png

Unsurprisingly the extra hand helps.

Gold Stake (Or Manacle)

At Gold Stake (or when facing Manacle) you are forced to play with a decreased hand size (7). If you are playing Gold Stake you are also subject to the blue stake debuff so have to play down a discard . I picked a few options to try out here too (including configurations with fewer discards because of the blue stake debuff).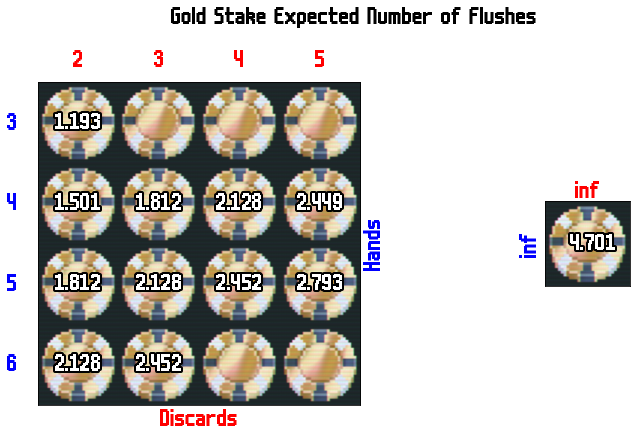

png

All the above results can shed some light on a few jokers that have us trade some of these parameters for others

Merry Andy and the Troubador

- Merry Andy: -1 Hand Size +3 Discards
- Troubadour: -1 Hand +2 Hand Size

From the above it looks like Merry Andy would decrease the expected number of playable flushes in the scenarios we solved. Troubadour Seems like it would increase the expected number of flushes in the above scenarios.

Another Joker we can solve some scenarios for is four fingers

Four Fingers

One interesting joker that affects playing flushes is Four Fingers. It makes it so that you only need 4 cards of the same suit to score a flush (and also the same for straights but we don't care about that here). We'll simulate playing with this one too.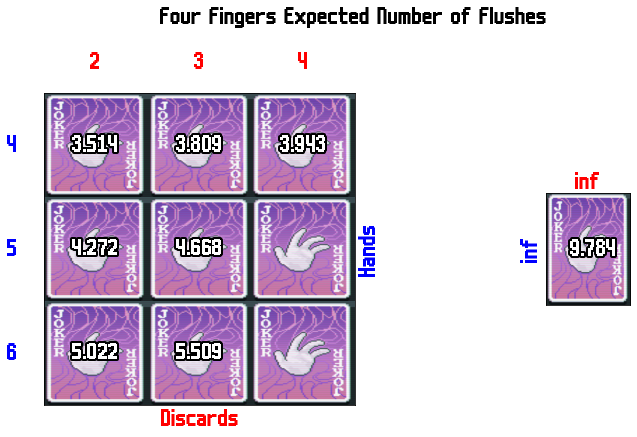

png

Suit Modification

Another way that players optimize their decks to play flushes is by modifying the suits of the cards in their deck.

Smear Joker / Checkered Deck

The checkered deck

And the smeared joker

both change your deck to having only two suits, which affects how easy it is to play a flush.

Below I solved for checkered deck with 8 card hand sizes.

png

A fun note is that checkered deck with 9 card hands doesn't need a solver.

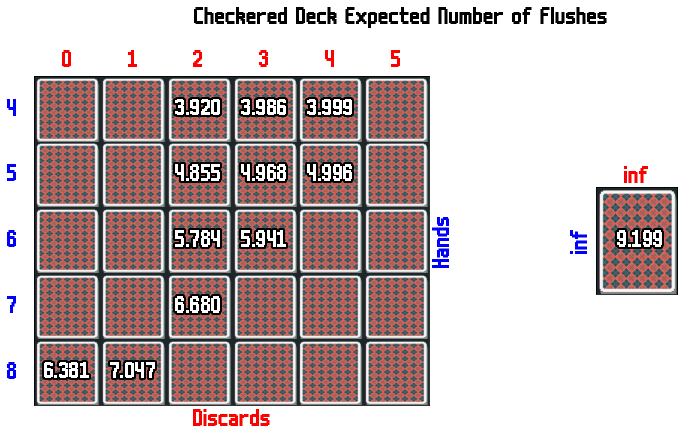
If you have 9 cards in hand and only 2 suits you will always be able to play a flush (one suit needs > 4 cards otherwise you can't have a 9 card hand)! The same is true with 7 or 8 card hands if you also have four fingers.

Tarot Cards

some tarot cards modify the suits of cards in your deck. There are 4 I looked at here (I'm ignoring lovers for now).

Star (Diamond), Moon (Club), Sun (Heart), World (Spade)

each of these changes up to 3 cards into a particular suit. I solved for the case where your deck is unmodified and then you use one of these. I tried a configuration where youu turn 3 cards of the same suit into another suit (1), and I also tried one where cards of 3 different suits are changed into the 4th suit (2).

png

So looks a little better in expectancy to do the first one

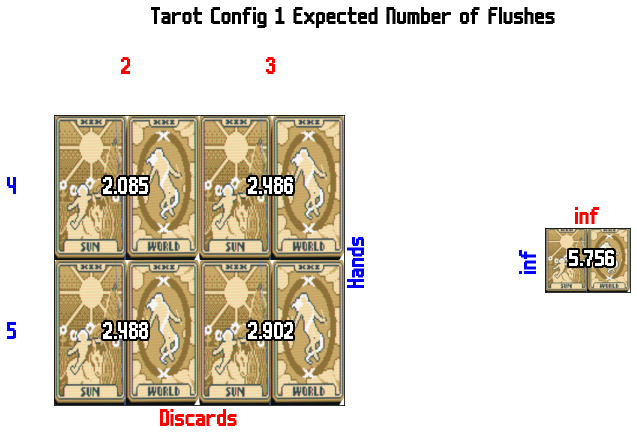
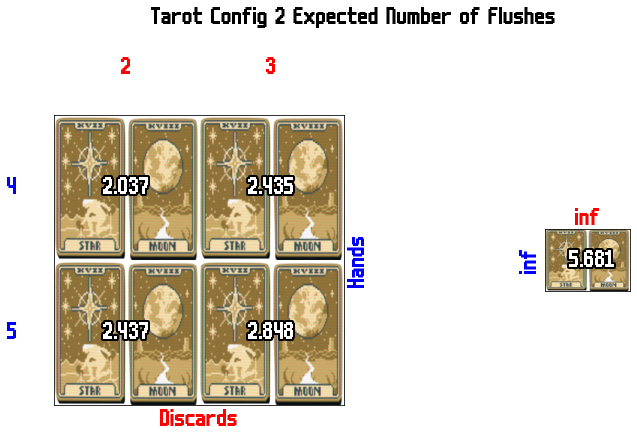
End

I guess nothing too surprising.

Looks like for the decks where its easier by default to play flushes the marginal hand helps more than the marginal discard. For the gold stake though they are pretty much equivalent.

Four fingers in many reasonable cases isn't as good as Smear Joker (or checkered deck) but if you had infinite hands and discards its better (maybe because using up only 4 cards for a flush helps in the long run?).

I guess the answer in general is expect to play 2-3 flushes. Sometimes more if your deck is strong otherwise less if it's weak.

Credits

Balatro: https://balatrogame.fandom.com/wiki/Balatro_Wiki

Font: https://managore.itch.io/m6x11